5.2.9 Skladanie harmonických vĺn. Stojaté vlny.

 

            Ako sme videli v odseku (5.2.2), z dvoch vĺn môžeme vytvoriť novú vlnu, ktorá je ich superpozíciou. Pre prípad harmonických vĺn takéto skladanie vedie k tzv. interferenčným javom. Interferenčné javy tvoria širokú triedu javov, ktorá bude podrobnejšie rozobratá v kapitole o vlnovej optike.

Teraz si všimneme superpozíciu dvoch harmonických vĺn s rovnakou amplitúdou, ktoré sa šíria navzájom opačným smerom. Predstavme si napríklad pozdĺžne vlny v pružnej tyči (rovnako dobre môžeme uvažovať strunu alebo vzduchový stĺpec). Spätná vlna môže napríklad vzniknúť odrazom na konci tyče.

Priama vlna bude vyjadrená

 

                                                                                               (5.2.9.1)

 

spätná bude daná

 

                                                                                               (5.2.9.2)

 

Pri sčítaní použijeme vzťah

 

                                                                       (5.2.9.3)

 

Sčítaním dostaneme

 

                                                                           (5.2.9.4)

 

čiže

 

                                                                                                   (5.2.9.5)

 

kde     

 

                                                                                                        (5.2.9.6)

 

            V každom bode máme teda harmonické kmitanie s uhlovou frekvenciou w a s amplitúdou /B(x)/, ktorá závisí od miesta. V miestach, kde B(x) je záporné, má okamžitá výchylka opačný smer oproti smeru okamžitých výchyliek v miestach s kladnou hodnotou B(x).

 


 

 


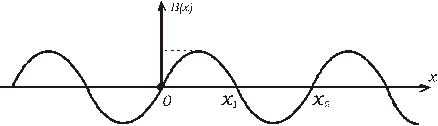
Obr. 5.2.9.1

 

 

Znázornime si priestorové rozdelenie výchyliek v čase t, keď sú výchylky maximálne, t. j. keď coswt = 1.

 

Miesta, kde B(x) = 0 sa vyznačujú nulovou amplitúdou kmitov, nazývame ich uzly. V miestach, kde /B(x)/ = max. je amplitúda kmitov najväčšia, nazývame ich kmitne. Pre uzol v mieste  x1 je  k.x1 = p, čiže

 

                                                                                                                    (5.2.9.7)

 

čiže

 

                                                                                                                        (5.2.9.8)

 

ostatné sú násobkami tejto hodnoty

 

                                                                          (5.2.9.9)

 

 

Kmitne sú v miestach s nepárnym násobkom λ/4  (pozri obr.(5.2.9.1))

 

                                                                           (5.2.9.10)

 

            Praktický spôsob upevnenia koncov struny je taký, že v koncových bodoch struny dĺžky l sú uzly. Teda

 

                                                                                 (5.2.9.11)

 

Ak sem dosadíme λ = v/f, dostaneme

 

                                                                                                 (5.2.9.12)

 

kde za rýchlosť šírenia vĺn na strune sme dosadili zo vzťahu (5.2.2.6).

Najnižšia frekvencia kmitania (tónu) struny je teda

 

                                                                                                               (5.2.9.13)

 

Tón s touto frekvenciou počujeme ako základný. Ostatné, odpovedajúce násobkom tejto základnej frekvencie, tzv. vyššie harmonické tóny, svojou prítomnosťou určujú zafarbenie základného tónu.

Vidíme, že základný tón závisí od sily P, ktorou je struna napínaná. Teda základný tón struny možno “ladiť” zmenou napínacej sily struny.

 

            Pre pružnú tyč (konečnej dĺžky l)obyčajne koncové body odpovedajú miestam s nulovým mechanickým napätím s = 0, teda podľa (5.2.3.7) musí byť v koncových bodoch tyče derivácia    u /   x  nulová. Odpovedá to kmitniam. Okrem toho ťažisko tyče je nehybné, preto protiľahlé konce sa pohybujú opačným smerom.

 

 


 

 

 


                                                                       Obr. 5.2.9.2

 

 

Teda

                                                                             (5.2.9.14)

 

Základná frekvencia kmitania sa teda vybudí, ak vlnová dĺžka vlnenia v tyči je práve taká, že platí  l = λ /2, ďalšie pre  l =3.( λ /2) atď., na dĺžku tyče teda pripadá nepárny počet polovĺn.

 

Kmitajúce vzdušné stĺpce majú praktické uplatnenie v píšťalách. Tieto môžu byť na oboch koncoch uzavreté, potom

 

                                                                                                                           (5.2.9.15)

 

alebo polootvorené (na jednom konci uzavreté, na druhom otvorené), potom

 

                                                                                                                (5.2.9.16)

 

V prípade píšťal, strún a tyčiek vznik stojatého vlnenia znamená súčasne výber frekvencií, ktoré môžu pri takomto vlnení existovať. Táto vlastnosť ostáva v platnosti aj pri iných druhoch vlnenia v ohraničenom prostredí, čo umožňuje konštrukciu tzv. rezonátorov.

 

Skladanie súbežných vĺn priestorovo posunutých.

Vezmime teraz  dve harmonické vlny, ktoré sa navzájom odlišujú len posunutím v smere osi x a vytvorme ich superpozíciu. Prvá vlna bude

 

                                                                                            (5.2.9.17)

 

a druhá bude posunutá o hodnotu posunutia D  za prvou vlnou. Ako už vieme, vyjadrenie tejto druhej vlny dostaneme, keď vo vzťahu (5.2.9.17) budeme namiesto x písať  x +D . Druhá vlna bude mať vyjadrenie

 

                                                                                   (5.2.9.18)

 

Potom použitie súčtového vzorca (5.2.9.3) dá

 

                                                                                     (5.2.9.19)

 

kde sme označili

 

                                                                                                          (5.2.9.20)

 

Vidíme, že výsledná vlna je opäť harmonická vlna s rovnakými hodnotami k a w s fázovým posunom k.D /2 . Jej amplitúda závisí od hodnoty B. Najväčšia amplitúda odpovedá situácii, keď argument funkcie kosínus v rov. (5.2.9.20) je celočíselným násobkom p. Teda

 

 

       kde  n  je celé číslo (alebo 0),                                               (5.2.9.21)

 

 

z čoho pre posunutie odpovedajúce maximálnej amplitúde zloženej vlny

 

                                                                                                                       (5.2.9.22)

 

To odpovedá situácii, keď druhá vlna je oproti prvej posunutá o celočíselný násobok vlnovej dĺžky. Vtedy priestorové rozdelenie výchyliek v obidvoch vlnách je rovnaké.       

Najmenšia (nulová) amplitúda výslednej vlny bude keď B je rovné nule. Argument funkcie kosínus v rov. (5.2.9.20) je vtedy nepárnym násobkom p /2 a dostaneme

 

,               kde n je celé číslo (alebo 0)                                                 (5.2.9.23)

 

čiže priestorové posunutie je nepárnym násobkom  l/2. To odpovedá situácii, kedy výchylky v prvej a druhej vlne sú navzájom opačné.

 

 


Príklad 5.2.5.  Ako sa zmení frekvencia tónu organových píšťal, ak sa teplota v koncertnej sále zvýši z pôvodnej teploty T0 = 295 K o hodnotu 2K ?

Riešenie :   Pre polootvorené píšťaly zo vzťahu (5.2.9.16) máme  f = v /4l  a za rýchlosť vĺn dosadíme vzťah z príkladu (5.2.4), potom

 

     ,

 

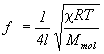 za teplotu dosadíme

 

 

 

 

  

 

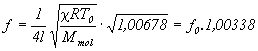
Frekvencia teda vzrastie o 0,34 % .

 

 

 


Kontrolné otázky k časti  5.2.9

1.     Ako vyniká stojaté vlnenie ?

2.     Čo sú uzly a kmitne ?

3.     Aké stojaté vlnenie môže existovať na strune s upevnenými koncami ?

4.     Aké stojaté vlnenie môže existovať v píšťalách ?

5.     Prečo sú pri  strunových nástrojoch hrubšie struny určené pre hlbšie tóny ?

6.     Vysvetlite, ako huslista (gitarista) skracovaním aktívnej dĺžky struny položením prsta mení frekvenciu a teda aj výšku tónu !

7.     Kedy dostaneme maximálnu a kedy minimálnu amplitúdu vlny pri skladaní dvoch harmonických súbežných vĺn s rovnakou amplitúdou, frekvenciou a vlnovou dĺžkou ?