5.2 Vlnenie

 

5.2.1 Úvod, charakteristika vlnenia

 

Osobitným prípadom pohybu v spojitom prostredí (kontínuu) je vlnenie. Predstavme si dokonale ohybné lano, napäté tak, že v stave pokoja je vo vodorovnej polohe. Úderom rukou alebo vhodným predmetom vyvolávame výchylku v okolí určitého miesta (Obr. 5.2.1.1)

 

 

 

 

 

                                                             Obr. 5.2.1.1

 

Zo skúsenosti vieme, že oblasť výchyliek neostáva v tých istých miestach, ale “beží” pozdĺž lana. Hovoríme, že pozdĺž lana sa šíri vlna (vlna výchyliek).

Za určitých ideálnych podmienok, ktoré preskúmame neskôr, sa tvar lana v oblasti výchyliek nemení, len oblasť priehybu sa posúva, premiestňuje. Aby sme to mohli popísať, stotožníme os  s lanom v stave pokoja.

Výchylku lana (v danom mieste a čase) označíme u, prípadne u(x,t), ak chceme explicitne vyjadriť, že závisí od x a t. Sledujme teraz len šírenie vlny smerom doprava (takisto bude potrebné vyšetriť šírenie smerom doľava). Ak rozloženie výchyliek v čase t=0 je popísané funkciou f(x), teda v mieste x výchylka sa rovná  f(x), môžeme napísať.

 

u(x,0) = f(x)                                                                                                                 (5.2.1.1)

 

Aká bude funkcia f(x) zavisí od toho, aké rozloženie výchyliek sme v čase t=0 úderom vyvolali. Ak v neskoršom čase t₁  budú všetky výchylky iba posunuté o hodnotu  l  doprava, bude toto rozloženie na osi  x  popísané tvarovo rovnakou funkciou  f(x), ale posunutou o  l . Z matematiky vieme, že posunutie grafu funkcie f(x) o hodnotu l v smere osi x dostaneme, ak vezmeme funkciu f(x-l), t.j. v  argumente pôvodnej funkcie miesto x vezmeme (x-l). Rozloženie výchyliek v čase t=0 a v čase t₁ je znázornené na Obr.

 

 

 

 

 

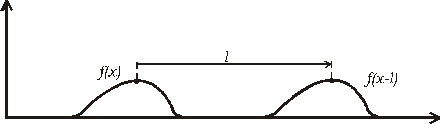
                                                             Obr. 5.2.1.2

                                     

 

Postupom času sa posunutie l zväčšuje. Ak je lano homogénne, dá sa očakávať, že rovnako veľké úseky prekoná vlna za rovnaký časový interval a teda posunutie l rovnomerne narastá s časom, l = vt, kde v má význam rýchlosti, s akou sa rozloženie výchyliek posúva v smere osi x. Rozloženie výchyliek, ako funkcia x a t, bude teda popísané funkciou

 

u(x,t) = f(x-vt).                                                                                                            (5.2.1.2)

 

Pre vlnu, bežiacu smerom doľava, musíme zmeniť znamienko v

 

u(x,t) = f(x+ vt).                                                                                                          (5.2.1.3)

 

Za akých podmienok nastane popísaný pohyb a aká môže byť funkcia f(x), ktorá popisuje rozloženie výchyliek (a teda vlastne tvar deformovaného lana), preskúmame neskôr.

        Podobný druh pohybu ako sme opísali vyššie, môžeme pozorovať na vodnej hladine. Ak vytvoríme úzky dlhý kanál všade s rovnakou hĺbkou, výchylky vodnej hladiny sa budú správať podobne ako výchylky lana v prípade, ktorý sme vyššie opísali – rozloženie výchyliek sa posúva v smere pozdĺž kanála. Takisto pri deformácii pružnej dlhej tyče v pozdĺžnom alebo priečnom smere pozorujeme podobné šírenie deformácii.

        Takéto vlny, ktoré sú spojené s pohybom hmotného prostredia, nazývame mechanické vlny. Ak výchylky častíc prostredia majú smer totožný so smerom šírenia vlny, nazývame ich pozdĺžne vlny. Ak sú výchylky kolmé na smer šírenia, používame názov priečne vlny.

        Existujú i vlny, ktoré nie sú spojené s mechanickým pohybom. Spomeňme ako príklad vlny, súvisiace so šírením rozloženia elektrického napätia na elektrickom vedení. Iným prípadom sú elektromagnetické vlny, kde namiesto výchyliek sledujeme priestorové a časové rozloženie elektrických a magnetických polí. Týmto sa však budeme zaoberať v inej časti tohoto kurzu.

        Vlnové procesy tvoria špecifickú skupinu javov a majú svoje spoločné zákonitosti, nezávisle na tom, v čom konkrétne sa vlny šíria. Preto často analýzu určitých vlnových procesov jedného typu je možno zovšeobecniť na širšiu triedu vlnových procesov.