5.2.6 Rovinné vlny. Rovinné harmonické vlny.                              

 

Vlny v pružnej tyči, šíriace sa v smere osi tyče, sa predsa len v jednom ohľade líšia od vĺn, ktoré sa šírili na strune.

 

 

Obr. 5.2.6.1

 

 

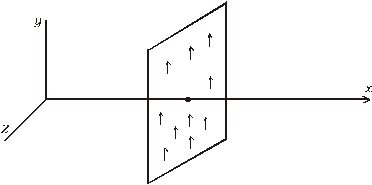
            V každom bode priečneho (kolmého) rezu tyče je okamžitá výchylka rovnaká. Ak si teraz predstavíme, že priečne rozmery tyče budeme zväčšovať tak, že sa postupne vyplní celý priestor, môžeme povedať, že v celých rovinách, kolmých na smer šírenia vlny je výchylka rovnaká.

 

 

 

Obr. 5.2.6.2

 

 

            Pre vlnu, šíriacu sa v smere osi x výchylka v bode (x, y, z) bude

 

                                                                                            (5.2.6.1)

 

čiže nezávisí od y, z. Výchylka v bode (x,y,z) je rovnaká, ako v bode (x,0,0). Takéto roviny, kolmé na smer šírenia nazývame vlnoplochy a spomínané vlny nazývame rovinné vlny. Ak je naviac funkcia f( ) harmonická, čiže je typu ako v (5.2.5.12), hovoríme o rovinnej harmonickej vlne.

            Uvažujme teraz vlnu, šíriacu sa v nejakom inom, ľubovoľne vybranom smere a hľadajme vyjadrenie takejto vlny.

 

 

Obr. 5.2.6.3

 

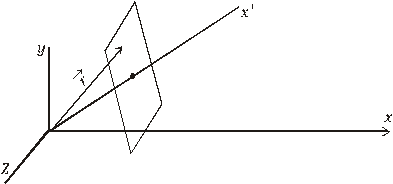
Nový smer šírenia stotožníme s osou x´ , jednotkový vektor v tomto smere označíme i ^`.

            Vyjadrenie priestorového a časového rozdelenia výchyliek bude ako vo vzťahu (5.2.5.12), v ktorom namiesto x budeme písať x´.

 

                                                                                         (5.2.6.2)

 

Pretože x^{`</sup> je vlastne súradnicou vektora r  vzhľadom na smer osi x<sup>`} (pozri Obr. 5.2.6.3), máme

 

x´  = i´∙r                                                                                                                       (5.2.6.3)

 

a

 

                                                                                                        (5.2.6.4)

 

            Rovinnú harmonickú vlnu, šíriacu sa v smere vektora k  a majúcu vlnovú dĺžku, určenú vzťahom

 

                                                                                                                      (5.2.6.5)

 

môžeme teda  popísať vzťahom

 

                                                                                        (5.2.6.6)

 

Pretože výchylka má aj smer, môžeme posledný vzťah zapísať aj vektorovo, ak pravú aj ľavú stranu vynásobíme jednotkovým vektorom v smere výchylky t:

 

                                                                       (5.2.6.7)

 

Smer jednotkového vektora t nazývame smerom polarizácie vlny. Ako už vieme, táto môže byť pozdĺžna alebo priečna.

Ak súčin k ∙r vo vzťahu (5.2.6.6) rozpíšeme v zložkách

 

                                                                                                (5.2.6.8)

 

potom priamo derivovaním rovnice (5.2.6.6) sa môžeme presvedčiť, že platí

 

                                                                                  (5.2.6.9)

 

ak pritom využijeme ešte vzťah medzi k a w, vzťah (5.2.5.11)

 

                                                                                        (5.2.6.10)

 

            Rovnica (5.2.6.9) popisuje už všeobecnejší prípad šírenia vĺn v rôznych smeroch. Budeme ju nazývať trojrozmernou vlnovou rovnicou. Je možné ju odvodiť podobne, ako sme to urobili pre jednorozmerný prípad s tým rozdielom, že teraz by bolo potrebné urobiť rozbor síl, pôsobiacich na objemový element prostredia, napríklad v tvare elementárneho hranola.

Riešením rovnice (5.2.6.9) sú aj guľové vlny, rozbiehajúce sa z jedného centra, pričom v malom okolí každého bodu sú blízke rovinným vlnám.

 

Kontrolné otázky k časti  5.2.6

1.     Vysvetlite pojem rovinná vlna !

2.     Čo je rovinná harmonická vlna ?

3.     Čo sú vlnoplochy ?

4.     Aká informácia o vlne je obsiahnutá vo vlnovom vektore ?

5.     Čo je  smer polarizácie vlny ?

6.     Čím sa odlišuje trojrozmerná vlnová rovnica od jednorozmernej ?

7.     Čo sú guľové vlny ?