5.2.3. Vlny v pružnej tyči

 

Podobne, ako sme v prípade struny analýzou podmienok v jej elemente dostali vlnovú rovnicu, vezmeme teraz pružnú tyč konštantného prierezu a budeme uvažovať výchylky častíc tyče v mieste x a v mieste x+Dx.

 

                                                                      

 

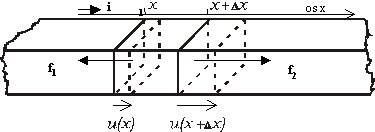
       Obr. 5.2.3.1  

 

 

Budeme najprv uvažovať pozdĺžne výchylky rovnaké v celých rezoch, vyznačených na Obr. 5.2.3.1.

 

Ak mechanické ťahové napätie v mieste x označíme s(x) a prierez tyče písmenom S, potom na vybraný element kladné (ťahové) napätie v mieste so súradnicou x+Dx pôsobí silou f₂, x-ová zložka ktorej i×f₂  je S.s(x+Dx), v mieste x silou f₁  s  x-ovou zložkou i×f₁, rovnou  –S.s(x) (prostredie naľavo od x “ťahá” element v opačnom smere). Ťažisko vybraného elementu sa nachádza vnútri intervalu (x, x+Dx), jeho x-ovú súradnicu označíme x_T, výchylka ťažiska teda bude u(x_T). Ak hustotu materiálu tyče označíme r, hmotnosť vybraného elementu bude

 

                                                                                                            (5.2.3.1)

 

Pohybová rovnica pre element tyče bude

 

                                                                              (5.2.3.2)

 

Ak dosadíme za Dm, po vykrátení S a delení Dx

 

                                                                              (5.2.3.3)

 

Ak teraz urobíme limitný prechod Dx®0, výraz na pravej strane prejde na deriváciu a dostaneme

 

                                                                                                         (5.2.3.4)

 

V tejto rovnici mechanické napätie závisí od x. Aby sme ho vyjadrili, použijeme Hookov zákon:

 

s = e.E,                                                                                                                       (5.2.3.5)

 

kde e je relatívne predĺženie pri danej deformácii, popísanej výchylkami u(x), E je modul pružnosti (ťahový). Relatívne predĺženie v danom mieste je tiež možné dostať tak, že najprv vezmeme element dĺžky Dx, vyjadríme jeho relatívne predĺženie, a potom urobíme prechod Dx®0. Pôvodná dĺžka elementu Dx sa vychýlením pravého konca zväčší o u(x+Dx) a posunutím ľavého konca o u(x) sa zasa zmenší o túto hodnotu. Zmena dĺžky elementu bude u(x+Dx)-u(x). Relatívne predĺženie dostaneme podelením tejto hodnoty pôvodnou dĺžkou Dx, čiže

 

                                                                                                (5.2.3.6)

 

V limite Dx®0 dostaneme opäť deriváciu

 

                                                                                                                       (5.2.3.6)

a teda mechanické napätie v mieste x je

 

                                                                                                              (5.2.3.7)

 

Dosadením do (5.2.3.4) dostaneme

 

                                                                                                        (5.2.3.7)

 

Túto rovnicu môžeme upraviť na nám už známy tvar, ak celú rovnicu delíme E a podiel  E/r označíme v²

 

                                                                                                                      (5.2.3.8)

 

Rovnica (5.2.3.7) potom prejde na tvar vlnovej rovnice, akú sme už dostali pre šírenie vĺn na strune (rovnica 5.2.2.7)

 

                                                                                                          (5.2.3.9)

 

Rýchlosť šírenia vĺn, spojených s výchylkami v pozdĺžnom smere je tu

 

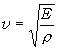                                                                                                                      (5.2.3.10)

 

Analýzu riešení rovnice (5.2.3.9) už teraz nemusíme robiť, pretože táto rovnica je tvarom zhodná s rovnicou (5.2.2.7), riešenia ktorej sme už rozoberali.

Rýchlosť šírenia vĺn je teraz určená modulom pružnosti E a hustotou tyče r. Teda tyče, vyhotovené z rôznych materiálov sa môžu vyznačovať rôznou rýchlosťou šírenia vĺn, závisí to od pomeru E/r.

 

Vlny, ktoré sme uvažovali pri odvodzovaní rovnice (5.2.3.9) sú spojené s výchylkou v pozdĺžnom smere, preto ich nazývame pozdĺžnymi vlnami.

            Podobne môžeme rozobrať prípad, keď výchylky elementov tyče by boli kolmé na os x. Celé odvodenie by bolo prakticky rovnaké s tým rozdielom, že teraz je element tyče deformovaný šmykom (skosený). V úvahe je preto treba použiť Hookov zákon pre prípad šmykového namáhania. Zopakovaním celej úvahy tak ako pri odvodzovaní vlnovej rovnice pre pozdĺžne vlny, by sme opäť dostali vlnovú rovnicu v tvare (5.2.3.9), avšak rýchlosť šírenia by bola

 

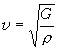                                                                                                                      (5.2.3.11)

 

kde G je modul pružnosti v šmyku. Vidíme teda, že rýchlosť šírenia priečnych vĺn je iná, obyčajne menšia, než rýchlosť pozdĺžnych vĺn.

            Vo všeobecnosti by sme mohli mať superpozíciu vĺn pozdĺžnych a priečnych, táto by sa však správala ináč, než ako bežné postupné vlny popísané rovnicou (5.2.2.8) alebo (5.2.2.18). Zložka, odpovedajúca pozdĺžnej vlne sa šíri inou rýchlosťou ako zložka, odpovedajúca priečnej vlne. Ak by sme napríklad vytvorili takúto superpozíciu v malej priestorovej oblasti, postupom času by sa pozdĺžna a priečna zložka vlny priestorovo oddelili, pretože každá postupuje inou rýchlosťou. Pôvodný tvar vlny by sa teda nezachovával.

 

 

Príklad 5.2.2.  Pri meraní rýchlosti pozdĺžnych aj priečnych vĺn sa často využíva ultrazvuk. Priestorove úzky vlnový útvar sa po prechode tyčou odráža od jej koncov a postupuje opačným smerom až ku druhému koncu tyče,tam sa opäť odráža atd. Na jednom konci tyče sa dopadajúca vlna sníma pomocou elektromechanického meniča, napríklad tenkej kremennej doštičky, prilepenej k tyči na jej koncovej čelnej ploche. Pri každom príchode (a odraze) vzniká na ňom elektrický napäťový impulz, ktorý sa zobrazuje na obrazovke osciloskopu. Vypočítajte ťahový modul pružnosti pre tyčku dĺžky  5 cm, ak časový interval medzi dvomi takýmito impulzami bol  19 ms. Hustota materiálu tyčky je  7800 kg.m ^–3 !

Riešenie :   Časový interval Δt odpovedá prachodu vlnového útvaru tam a nazpäť.Ak dĺžku tyčky označíme l, potom

                                              

, 

a podľa vzťahu (5.2.3.10) je po umocnení  

 

 ,

 

teda   

  .

Po dosadení

 

                                              

 

 

Kontrolné otázky k časti  5.2.3

1.   Vysvetlite význam jednotlivých členov v rovnici (5.2.3.2) !

2.   Prečo v rovnici vystupuje zrýchlenie ťažiska a nie iného bodu ?

3.   Prečo potrebujeme Hookov zákon pre bilanciu síl, pôsobiacich na element tyče ?

4.   Kedy je  ε v rovnici (5.2.3.6) malé ?

5.   Aké druhy polarizácie mechanickej vlny poznáme?

6.   Od čoho závisí rýchlosť šírenia pozdĺžnych a priečnych vĺn ?

7.   Ktoré veličiny je možné vypočítať z nameraných hodnôt rýchlosti pozdĺžnych a priečnych vĺn ?

8.   Čo nastane pri superpozícii pozdĺžnej a priečnej vlny v tyči?