5

 

MECHANICKÉ KMITANIE A VLNENIE

 

5.1 Kmitanie

 

       Periodické pohyby častíc a telies ako celkov, nazývame kmitanie. Príkladom kmitavého pohybu je pohyb guľôčky zavesenej na pružine, kyvadlový pohyb fyzikálneho, matematického alebo torzného kyvadla. Matematická funkcia, ktoré opisuje kmit, je funkciou času. Ak táto funkcia je harmonická, t. j. sínus alebo i kosínus, hovoríme o harmonických kmitoch. Ľubovoľný kmitavý pohyb môžeme podľa Fourrierovej vety vyjadriť ako superpozíciu harmonických kmitov so základnými frekvenciami a ich celočíselnými násobkami. Z tohto dôvodu môžeme harmonické kmity považovať za základný typ periodického pohybu.

       Ak sústavy kmitajú s frekvenciami určenými parametrami sústavy, hovoríme o vlastných kmitoch. Ak sa uplatňujú sily, ktoré amplitúdu kmitavého pohybu zmenšujú, hovoríme o tlmených kmitoch. Keď vonkajšie sily vynucujú ich kmitanie s odlišnými frekvenciami, hovoríme o vynútenom kmitaní. Teleso vykonávajúce harmonický kmitavý pohyb nazývame harmonický oscilátor. Pohybová rovnica harmonického oscilátora je diferenciálna rovnica. Táto rovnica sa vo fyzike objavuje veľmi často a opisuje napr. kmity náboja v elektrickom obvode, kmity ladičky vytvárajúce zvukové vlny, vibrácie elektrónov v atóme vytvárajúce svetelné vlny, správanie sa termostatu pri regulácii teploty, atď. Tieto rovnice sú lineárnymi diferenciálnymi rovnicami s konštantnými koeficientmi.

 

5.1.1 Harmonický oscilátor

 

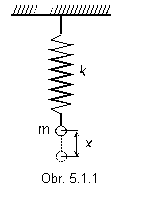
       Ako harmonický oscilátor môže byť v prvom priblížení guľôčka na pružinke (obr. 5.1.1). Pružinka sa najprv napne, aby vyvážila gravitačnú silu. Keď nastane rovnováha, zaujímame sa o vertikálnu výchylku, ktorú si označíme x. V tomto prípade sila, ktorá spôsobí výchylku, je priamoúmerná výchylke

       F = - kx ,                                                                                                         (5.1.1)

kde k je konštanta úmernosti a k > 0. Znamienko mínus je preto, lebo sila pôsobí opačným smerom ako výchylka.

       Pohybová rovnica harmonického oscilátora berúc do úvahy rovnicu (5.1.1) má tvar

       ,                                                                            (5.1.2)                                                                                                                                                                                                                                                                                                                            

ktorú môžeme upraviť na normovaný tvar

        ,                                                                                          (5.1.3)                                                                                                                                                                                                                                                                                                                            

kde

  

je uhlová frekvencia vlastných kmitov, m je hmotnosť guľôčky.

       Ako sa ľahko môžeme presvedčiť, riešením tejto rovnice sú funkcie  A cos w ₀t  a  B sin w ₀t , kde A a B sú nezávislé konštanty. Z teórie matematickej analýzy vyplýva, že aj ich lineárna kombinácia je riešením rovnice (5.1.3)

        ,                                                                             (5.1.4)                                                                                                                                                                                                                                                                                                                            

a pre rýchlosť platí

        .                                                         (5.1.5)                                                                                                                                                                       

Integračné konštanty A a B sú určené začiatočnými podmienkami, t. j. polohou x (0) a rýchlosťou v (0) v čase t = 0.

       Perióda kmitavého pohybu je

        ,                                                                                      (5.1.6)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

a frekvencia

        ,                                                                                       (5.1.7)                                                                                                                                                                                                                                                                                                                            

       Perióda kmitavého pohybu nezávisí od toho, ako sa pohyb začal, nezávisí teda od začiatočných podmienok.

       V skutočnosti od tohto všeobecného riešenia rovnice (5.1.3) existujú aj iné formy zápisu riešenia. Pomocou substitúcie A= x₀ sin j a B = x₀ cos j riešenie (5.1.4) môžeme vyjadriť v tvare

       ,                                                                                    (5.1.8)                                                                                                                                                                                                                                                                                                                            

a rýchlosť

       ,                                                                               (5.1.9)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

kde x₀ určuje maximálnu dosiahnutú výchylku a nazýva sa amplitúda kmitov. Výraz (w₀ t+j) sa nazýva fáza kmitania a j fázová konštanta, ktorú určíme zo začiatočných podmienok.

      

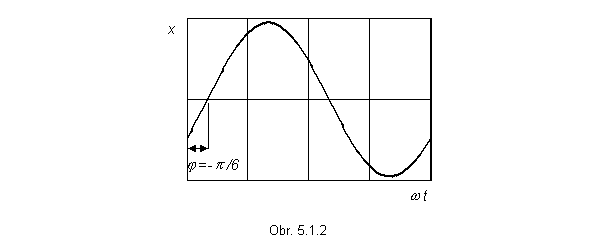
Grafickým obrazom pohybu harmonického oscilátora je sínusoida s amplitúdou x₀, periódou T s fázou v čase t = 0 posunutou o konštantu j (obr.5.1.2).

       Celková energia harmonického oscilátora sa skladá z jeho kinetickej energie

       ,                                                  (5.1.10)                                                                                                                                                                       

a potenciálnej energie

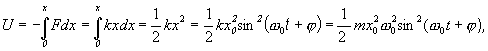  (5.1.11)           

pričom sme použili vzťah

 .

Celková energia je súčtom kinetickej (5.1.10) a potenciálnej energie (5.1.11)

       .                                                                             (5.1.12)                                                                                                                                                                                                                                                                                                                     

       Celková energia je konštantná, pretože zmeny kinetickej energie sú opačné ako zmeny potenciálnej energie.

 

Príklad 5.1.1  Určite amplitúdu a fázovú konštantu netlmeného harmonického oscilátora, ak v čase  t =0  sa vyznačuje výchylkou x(0) = 0,1 m a rýchlosťou v(0) = 0,2 ms^-1, keď frekvencia f = 1 Hz.

Riešenie: Pre výchylku x(0) a rýchlosť v(0) v čase t = 0 podľa vzťahov (5.1.8) a (5.1.9) platí

 

                                 

      

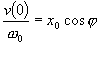
Umocnením rovníc a sčítaním dostaneme

      

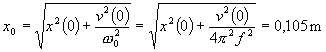
a delením rovníc

      

čiže j = 72°20^`.

 

5.1.2 Kyvadlá

       Fyzikálne kyvadlo je teleso upevnené tak, že sa môže otáčať okolo vodorovnej osi, ktoré neprechádza ťažiskom (obr. 5.1.3). Ak vzdialenosť jeho ťažiska od osi otáčania je a a teleso má hmotnosť m, pri výchylke z rovnovážnej polohy na teleso pôsobí jeho tiaž G = mg, ktorá vzhľadom na os otáčania vyvoláva moment sily

       ,                                                                                       (5.1.13)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

kde a je výchylka z rovnovážnej polohy. Znamienko mínus vystihuje skutočnosť, že moment sily je opačne orientovaný ako výchylka a. Ak fyzikálne kyvadlo vychýlime z rovnovážnej polohy a uvoľníme, rozkmitá sa.

      

 

 

 

 

 

 

 

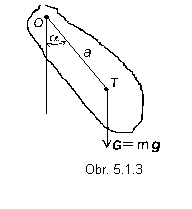
Fyzikálne kyvadlo vykonáva okolo osi rotačný pohyb, pre ktorý platí pohybová rovnica

       ,                                                                                        (5.1.14)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

kde J je moment zotrvačnosti telesa vzhľadom na os otáčania a

 

 je uhlové zrýchlenie a po dosadení rovnice (5.1.13) do rovnice (5.1.14) získame pohybovú rovnicu fyzikálneho kyvadla

.                                                                                      (5.1.15)                                                                                                                                                                                                                                                                                                         

Ak sa obmedzíme len na malé kmity kyvadla (na kmity s maximálnou výchylkou neprevyšujúcou 5°, t. j. asi 0,1 rad), vtedy platí   (rozdiel je menší ako 0,00011), kde uhol a je vyjadrený v radiánoch.

Za uvedenej podmienky dostaneme pohybovú rovnicu v tvare

       ,                                                                                     (5.1.16)                                                                                                                                                                                                                                                                                                                            

ktorá je totožná s rovnicou pre harmonický oscilátor (5.1.3) pre

 .

       Riešením tejto rovnice podobne ako v prípade harmonického oscilátora môžeme napísať v tvare

       ,

kde a₀ je maximálna výchylka kyvadla. Pre periódu kmitavého pohybu (dobu kmitu) platí podľa (5.1.6)

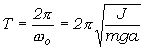        ,                                                                                (5.1.17)                                                                                                                                                                                                                                                                                                                            

a frekvenciu

       .                                                                                  (5.1.18)                                                                                                                                                                                                                                                                                                                     

       Z uvedených vzťahov vyplýva, že ak poznáme periódu kmitavého pohybu (dobu kmitu) telesa kmitajúceho ako fyzikálne kyvadlo, dokážeme zmerať jeho moment zotrvačnosti.

 

Príklad 5.1.2  Určite moment zotrvačnosti telesa hmotnosti m = 1 kg, ktoré kmitá okolo vodorovnej osi ako fyzikálne kyvadlo s periódou T = 1s, ak vzdialenosť osi kývania od ťažiska a = 0,1 m.

Riešenie: Z rovnice (5.1.17) vyplýva pre moment zotrvačnosti vzťah

       .

 

Matematické kyvadlo si možno predstaviť ako malú gulôčku zavesenú na tenkej niti. Prísne vzaté, je to hmotný bod zavesený na nehmotnom závese. Je jasné, že takto zavedený pojem je len hraničná abstrakcia. Na matematické kyvadlo sa môžeme pozerať aj ako na špeciálny prípad fyzikálneho kyvadla, ktoré degenerovalo len na jeden hmotný bod ležiaci mimo osi rotácie. Keď hmotnosť hmotného bodu je m a dĺžka závesu l, vtedy J = ml² a vzdialenosť ťažiska od osi otáčania (upevnenia závesu) je tiež l. Pre periódu matematického kyvadla platí

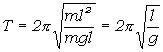       .                                                                            (5.1.19)                                                                                                                                                                                                                                                                                                                     

Dĺžka matematického kyvadla, ktoré kýva s rovnakou dobou kmitu ako určité fyzikálne kyvadlo, sa nazýva redukovaná dĺžka tohoto fyzikálneho kyvadla a platí vzťah

.

Torzné kyvadlo je teleso zavesené na zvislom pružnom vlákne tak, že jeho os súmernosti splýva s vláknom (obr. 5.1.4). Ak zotrvačník torzného kyvadla vytočíme z jeho rovnovážnej polohy o uhol a, skrútené vlákno účinkuje na zotrvačník dvojicou síl, ktorá je pri malých výchylkách úmerná uhlu a a ktorá sa snaží vrátiť zotrvačník späť do jeho rovnovážnej polohy. Moment dvojice síl je

       ,                                                                                                  (5.1.20)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

kde konštanta úmernosti D₀ sa nazýva direkčný moment.

       Pre rotačný pohyb zotrvačníka platí pohybová rovnica

       .                                                                        (5.1.21)                                                                                                                                                                                                                                                                                                                     

 

      

 

 

 

 

 

 

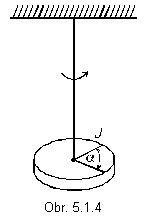
Po úprave získame pohybovú rovnicu torzného kyvadla v normovanom tvare

       .                                                                                        (5.1.22)                                                                                                                                                                                                                                                                                                                            

Riešenie rovnice torzného kyvadla je také isté ako v prípade fyzikálneho kyvadla

       .

Perióda torzného kyvadla je daná vzťahom

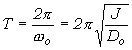         ,                                                                                  (5.1.23)                                                                                                                                                                                                                                                                                                                            

a frekvencia

         .                                                                                    (5.1.24)                                                                                                                                                                                                                                                                                                                                                                                                                                                              

       Metódou torzného kyvadla môžeme určovať moment zotrvačnosti telies a merať modul pružnosti v šmyku (torzii) pružného vlákna.

 

Príklad 5.1.3  Na kruhovú dosku torzného kyvadla, ktoré má hmotnosť m = 0,5 kg a polomer 

r = 0,1m, položíme teleso, ktorého moment zotrvačnosti chceme určiť Pôvodná perióda torzného kyvadla T₀ = 1s sa zmení po priložení telesa na T₁ = 1,5 s. Určte moment zotrvačnosti skúmaného telesa!

Riešenie: Pre moment zotrvačnosti torzného kyvadla zo vzťahu (5.1.23) vyplýva, že

                a          ,

kde

 

je moment zotrvačnosti kruhovej dosky torzného kyvadla a J₁ je moment zotrvačnosti torzného kyvadla s priloženým telesom. Z uvedených vzťahov vyplýva, že

 

        .

Moment zotrvačnosti J₁ = J₀ + J_x, kde J_x je moment zotrvačnosti skúmaného telesa. Pre J_x potom platí

       .

 

5.1.3 Tlmené kmity

       Pri harmonickom oscilátore a kyvadlách popísaných v predchádzajúcich častiach, sme neuvažovali s odporom prostredia. Celková energia harmonického oscilátora ostávala konštantná. Každé reálne kmitanie sústav je však tlmené. Ak sústavne nedodávame energiu, amplitúda kmitov sa zmenšuje a klesá až na nulu. Príčinou je odporová sila prostredia F_b pôsobiaca proti pohybu. Pri malých rýchlostiach býva brzdná sila úmerná rýchlosti, t. j. v prípade harmonického oscilátora

        ,                                                                                  (5.1.25)

kde k_b je konštanta úmernosti a k_b > 0.

       Celková sila pôsobiaca na tlmený harmonický oscilátor

        ,                                                                                      (5.1.26)

čo vedie k pohybovej rovnici

        .                                                                          (5.1.27)

       Zavedieme si veličinu b = k_b/2m, ktorá sa nazýva koeficient tlmenia a

        

(uhlová frekvencia vlastných kmitov netlmeného harmonického oscilátora). Použitím uvedených veličín dostaneme normovanú pohybovú rovnicu tlmeného harmonického oscilátora

        .                                                                              (5.1.28)

       Riešenie diferenciálnej rovnice (5.1.28) možno hľadať v tvare

        .

Dosadením tejto funkcie do rovnice (5.1.28) dostaneme pre parameter a charakteristickú rovnicu

        ,                                                                                 (5.1.29)

ktorá má dva korene

       .

       Partikulárne riešenia rovnice (5.1.28) sú teda

                    a             ,

kde A, B sú ľubovoľné konštanty. Pretože diferenciálna rovnica (5.1.28) je lineárna a homogénna, riešením rovnice je aj súčet riešení

        .                                                                                      (5.1.30)

       Priebeh tlmeného pohybu harmonického oscilátora závisí od toho, či charakteristická rovnica (5.1.29) má dva korene imaginárne, jeden koreň dvojnásobný, alebo dva korene reálne.

 

Periodický pohyb.

Pri malom tlmení je

a korene a₁, a₂ sú komplexné. Pretože charakteristická rovnica (5.1.29) má riešenie

,

kde

 

je uhlová frekvencia tlmeného harmonického oscilátora. Dá sa dokázať, že riešením rovnice (5.1.28) sú reálne funkcie ,

ako aj

.

To isté platí aj pre druhý koreň a₂, získame teda štyri funkcie, ktoré sú riešením diferenciálnej rovnice (5.1.28). Z nich sú len dve lineárne nezávislé, pretože

 a    .

Riešenie rovnice (5.1.28) môžeme teda napísať v tvare

       ,                                                                 (5.1.31)

kde A a B sú konštanty, ktoré môžeme určiť zo začiatočných podmienok. Použitím substitúcií podobných ako v prípade netlmeného harmonického oscilátora,  A = x₀ sin j a B =x₀ cos j, dostaneme riešenie rovnice (5.1.28) v tvare

       ,                                                                                  (5.1.32)

 

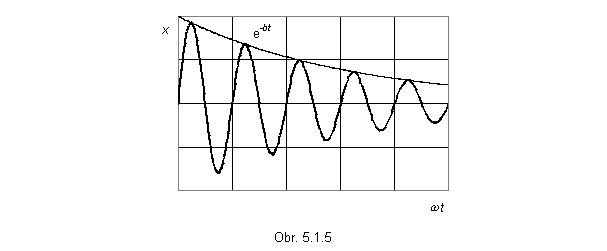
kde x₀ je maximálna výchylka a j je fázová konštanta (obr. 5.1.5).

      

       Za mieru tlmenia tlmeného pohybu možno považovať koeficient tlmenia b. Inou charakteristickou veličinou, ktorá charakterizuje tlmenia kmitavého pohybu je útlm l, definovaný ako podiel výchylky v čase t a výchylky v čase t + T. Platí

 

       .                                                          (5.1.33)

       Ďalšou veličinou charakterizujúcou tlmenie je logaritmický dekrement definovaný

        .                                                                                           (5.1.34)

Koeficient tlmenia b sa ľahko vypočíta z útlmu l a periódy T

        .                                                                                            (5.1.35)

B. Aperiodický pohyb. Pri veľkom tlmení  a korene charakteristickej rovnice

       ,

kde

       ,

sú reálne a riešenie rovnice (5.1.18) môžeme napísať v tvare

       .                                                                             (5.1.36)

       Z grafického priebehu funkcie (obr. 5.1.6) vidíme, že nevzniká periodický priebeh.

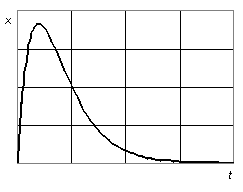
C. Hraničný pohyb. Pohyb sa stáva aperiodickým, keď

 

 V tomto prípade má charakteristická rovnica jediný dvojnásobný koreň a = -b a riešenie má tvar

Obr. 5.1.7

       .                                                                                       (5.1.37)

      

 

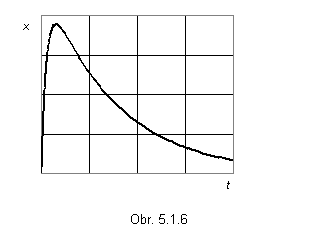
Vidíme, že v čase t = - A/B je x = 0, takže oscilátor sa vráti do rovnovážnej polohy     (obr. 5.1.7).

 

Príklad 5.1.4  Logaritmický dekrement tlmených harmonických kmitov d = 0,02. Vypočítajte, koľkokrát sa zmenší amplitúda kmitov po 100 kmitoch.

Riešenie: Zo vzťahu (5.1.32) vyplýva, že pre podiel výchylky v čase t a výchylky v čase t+100T platí

       .

 

5.1.4. Vynútené kmity

       Ak zoberieme doslovne nadpis paragrafu, každé kmitanie je vynútené, lebo nijaká sústava sa sama od seba nerozkmitá. musíme jej dodať nejakú energiu, aby sa rozkmitala.

       Pod pojmom vynútené kmity budeme chápať kmitanie pri trvalom pôsobení vonkajšej periodickej sily na kmitavú sústavu. Ďalej sa budeme venovať tlmenému harmonickému oscilátoru, na ktorý bude pôsobiť vonkajšia sila

       ,                                                                                         (5.1.38)

kde F₀ je amplitúda vonkajšej sily a w_v uhlová frekvencia vonkajšej sily.

       Na harmonický oscilátor budú pôsobiť tri sily:

1)     sila pružnosti,   F_p = - kx,

2)     tlmiaca sila    ,

3)     vonkajšia sila   F_n = F₀ sin w_n t.

Celková sila F pôsobiaca na harmonický oscilátor je

        ,                                                                      (5.1.39)

čo vedie k pohybovej rovnici

       ,                                                                (5.1.40)

pričom v zhode s predchádzajúcim paragrafom sme si označili

                           

       Pohybová rovnica (5.1.40) je diferenciálna rovnica 2. rádu s konštantnými koeficientami s pravou stranou. Podľa pravidiel matematickej analýzy riešenia tejto rovnice môžeme napísať ako riešenie bez pravej strany, t. j. funkcie (5.1.32) a partikulárneho integrálu

       ,                                                                             (5.1.41)

kde konštanty x_m a j_v musíme zvoliť tak, aby rovnica (5.1.40) bola splnená.

       Všeobecné riešenie môžeme preto napísať v tvare

       ,                                             (5.1.42)

kde prvý člen predstavuje vlastné kmity, ktoré po určitom čase zaniknú   (t > 1/b). Jedná sa o tzv. prechodový jav. Druhý člen (5.1.42) predstavuje tzv. ustálené kmitanie harmonického oscilátora, ktorý kmitá s frekvenciou vonkajšej sily w_v. Konštanty x_m a j_v nájdeme tak, že funkciu (5.1.41) dosadíme do rovnice (5.1.40) a dostaneme rovnicu

(5.1.43)

Keď v tejto rovnici rozpíšeme sin (w_v t - j_v) a cos (w_v t - j_v) podľa známych vzťahov a porovnáme koeficienty pri funkciách sin w_vt a cos w_vt, dostaneme pre konštanty x_m a j_v dve rovnice

       ,                                            (5.1.44)

       .                                                          (5.1.45)

Z nich vyplýva

       ,                                                                                            (5.1.46)

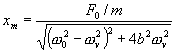       .                                                                         (5.1.47)

       Z rovnice (5.1.46) a (5.1.47) vyplýva, že v rezonancii, t. j. ak  w_v ® w₀, je fázové posunutie kmitov za vynucujúcou silou j _v  = p/2 a pri malom tlmení b amplitúda kmitov x_m rastie nad všetky medze (obr. 5.1.8). Z obrázka je vidieť, že najväčšia amplitúda kmitov je pri rezonančnej frekvencií a amplitúda kmitov závisí od veľkosti tlmenia.

       Rezonančné kmitanie pružných rezonančných sústav najmä pri malom tlmení, môže viesť až k deštrukcii sústavy (napr. strojov, budov, mostov, atď.). Na druhej strane je na tomto princípe založený prístroj na meranie otáčok. Oveľa širšie je využitie rezonančného javu v oblasti elektrických javov (elektrický oscilačný obvod), ktorý sa využíva pri prenose správ. Rovnica elektrického oscilačného obvodu je identická s rovnicou (5.140).

 

Príklad 5.1.5  Aká je rezonančná amplitúda harmonického oscilátora, ktorý koná vynútené kmity, keď jeho hmotnosť m = 0,1kg, uhlová frekvencia vlastných kmitov w₀ = 10 s^-1 a amplitúda vynucujúcej sily F = 5 N. Vypočítajte aj rezonančnú kruhovú frekvenciu!

Riešenie: Pre amplitúdu harmonického oscilátora konajúceho vynútené kmity podľa vzťahu (5.1.47)

       .

Amplitúda x_m bude maximálna pri rezonancii, keď platí

,

 t. j. menovateľ bude minimálny

 .

Pre hľadanú rezonančnú kruhovú frekvenciu z tejto rovnice vyplýva

      

a pre rezonančnú amplitúdu

       .

 

       Skutočnosť, že na popis mechanických a elektrických kmitavých sústav sa používajú identické diferenciálne rovnice, viedli k tomu, že na simuláciu (chovanie) zložitých mechanických sústav (napr. nápravy automobilov s pružinami a tlmičmi) sa používa ekvivalentná elektrická sústava zložená z odporov, cievok a kondenzátorov.

       V elektrických obvodoch sa ľahšie menia parametre sústavy a prípadná deštrukcia je menej bolestná ako v prípade mechanickej sústavy.

 

5.1.5 Skladanie kmitavých pohybov

       V praxi sa často stretávame s prípadom, že na hmotný bod pôsobia dve s časom periodicky sa meniace sily. Výsledný pohyb hmotného bodu je potom zložený z kmitov, ktoré odpovedajú jednotlivým silám. Z technického hľadiska je zaujímavé skladanie kmitov rovnakého smeru a skladanie kmitov, ktoré sú na seba kolmé.

A. Skladanie kmitavých pohybov na priamke.

       Uvažujeme dve kmitania

        ,                                                                             (5.1.48)

        ,                                                                           (5.1.49)

prebiehajúce pozdĺž osi x. Výsledný kmitavý pohyb bude súčtom jednotlivých kmitov

       .                             (5.1.50)

       Výsledný priebeh kmitania bude všeobecne zložitý. Maximálna výchylka výsledného pohybu neprekročí x₀₁ + x₀₂, lebo hodnota funkcie sinus sa rovná nanajvýš 1. V prípade, ak    x₀₁ = x₀₂ = x₀, w₁ = w₂ = w a j₁ = j₂ = j, dostaneme

        .                                                                                (5.1.51)

Amplitúda výsledného pohybu bude dvojnásobná. V prípade, ak rozdiel fázových konštánt 

j₁ - j₂ = p, platí

        ,                                     (5.1.52)

lebo sin(wt + j₂ + p) = - sin(wt + j).

 

 

V tomto prípade sa budú dve kmitania rušiť.

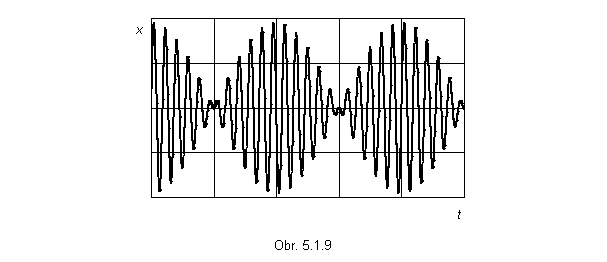
       Zaujímavý prípad skladania kmitov nastane pri skladaní kmitov s rovnakou amplitúdou a málo sa líšiacimi uhlovými frekvenciami w₁ a w₂ (obr. 5.1.9). Na výsledné kmitanie sa možno pozerať ako na kmitanie s kolísaním intenzity amplitúdy (rázy). Za predpokladu, že x₀₁ = x₀₂ = x₀ a j₁ = j₂ = 0, výsledný kmitavý pohyb je opísaný funkciou

        .                                                     (5.1.53)

Keď použijeme známu súčtovú vetu z trigonometrie, môžeme funkciu (5.1.53) napísať v tvare

       .                                                      (5.1.54)

Takýto pohyb je vo všeobecnom prípade zložitý neharmonický pohyb, ale ak rozdiel w₁ - w₂ je malý, môžeme ho považovať za harmonický pohyb s výslednou uhlovou frekvenciou

        ,                                                                                             (5.1.55)

ktorého amplitúda

                                                                                       (5.1.56)

sa mení s časom. Pre periódu kolísania intenzity kmitania (rázy) platí

        ,                                                                                            (5.1.57)

z čoho pre frekvenciu  f_r rázov platí f_r = f₁ – f₂  .   Ak sa jedna frekvencia blíži k druhej, frekvencia rázov sa zmenšuje a pri rovnosti frekvencií rázy zaniknú.

 

Príklad 5.1.6 Dva rovnobežné kmitavé pohyby rovnakej amplitúdy, rovnakej fázovej konštanty a blízkych periód T₁ = 10 s a T₂ = 10,1 s sa skladajú do výsledného kmitavého pohybu. Vypočítajte periódu výsledného kmitavého pohybu a periódu rázov.

Riešenie:  Zo vzťahu (5.1.55) vypočítame periódu výsledného kmitavého pohybu

      

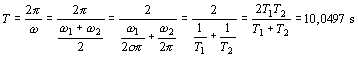
a zo vzťahu (5.1.57) vyjadríme periódu rázov

       .

 

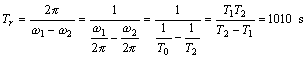B. Skladanie navzájom kolmých kmitov.

       Prvý kmitavý pohyb prebieha v smere osi x,

        ,                                                                                (5.1.58)

druhý v smere osi y,

 

      

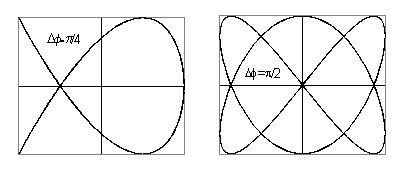
 .                                                                                     (5.1.59)

      

       Vo všeobecnosti dostávame zložité krivky. V prípade, že pomer uhlových frekvencií w₁ a w₂ je racionálne číslo, nazývame krivky Lissajussove krivky (obr. 5.1.10) Ak frekvencie a amplitúdy kmitov budú rovnaké, t. j. w₁ = w₂ = w, x₀ =

môžeme vzťahy (5.1.58) a (5.1.59) napísať v tvare

       ,                                                                                    (5.1.60)

        .                                             (5.1.61)

       Príslušná Lissajoussova krivka bude mať tvar kružnice, lebo umocnením rovníc (5.1.60) a (5.1.61) a ich sčítaním, dostaneme

       ,

čo predstavuje rovnicu kružnice o polomere A.

       Ak amplitúdy x₀ a y₀ nie sú rovnaké a pre fázové konštanty platí j₂ = j₁ + p, pohyb bude prebiehať po priamke

       ,                                                                                  (5.1.62)

       .                                           (5.1.63)

Ak podelíme rovnice (5.1.62) a (5.1.63), dostaneme rovnicu priamky

        .

       Všeobecne môžeme povedať, že skladaním dvoch na seba kolmých kmitov s rovnakou frekvenciou dostaneme elipsu, kružnicu alebo úsečku.

       Lissajoussove krivky sa využívajú na určenie pomeru frekvencii a zisťovanie fázového rozdielu, najmä v elektrotechnike pomocou osciloskopu.