5.2.8 Huygensov princíp. Odraz a lom na rovinnom rozhraní.

 

            Pri rozbore šírenia vĺn v  jednorozmerných prípadoch sme videli, že existencia vlny v jednom okamihu je vlastne príčinou jej ďalšej existencie v neskorších okamihoch. Priestorové rozloženie výchyliek v okolí zvoleného bodu sa za časový interval Dt celé premiestni o vzdialenosť v.Dt. Podobne je to aj pri šírení vĺn v dvojrozmernom či trojrozmernom prostredí.

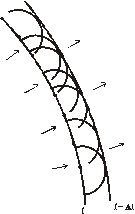
Podľa Huygensa každý bod, kde v určitom okamihu existuje vlna, stáva sa zdrojom vlnenia pre neskoršie časové okamihy.

 

 

 

 

                                                                          Obr. 5.2.8.1

 

Predstavme si, že vlna sa v čase t dostala až po určitú vlnoplochu, ktorú nazveme čelo vlny (obr. 5.2.8.1). Z každého bodu čela vlny sa šíri guľová vlna, ktorá sa za časový interval Dt dostane do vzdialenosti v.Dt. Novú polohu čela vlny v čase t+Dt dostaneme jako obálku takto zostrojených guľových vlnoplôch.

                                                       

 

Huygensov princíp poskytuje teda jednoduchú metódu, ako konštruovať novú vlnoplochu. Metóda však nehovorí, ako sa zmení amplitúda vlny.

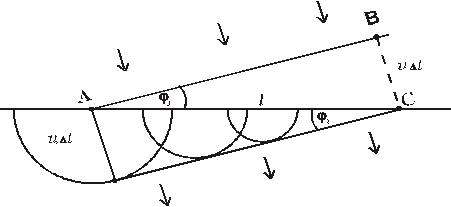
Overme si účinnosť tejto metódy na prípade lomu pri prechode rovinnej vlny cez rovinné rozhranie. Nech rovinná vlna prichádza z prostredia, kde rýchlosť šírenia vlny je v₁, a dopadá na rovinné rozhranie s druhým prostredím, kde rýchlosť šírenia je v₂. Čelo dopadajúcej vlny zviera s rozhraním uhol φ₁. (Obr. 5.2.8.2)

 

 

                                                                  Obr. 5.2.8.2

 

V bode A už čelo vlny dorazilo na rozhranie, zatiaľ čo bod B vlnoplochy sa dostane na rozhranie (do bodu C) až o Dt neskôr. V okamihu, keď na rozhranie dopadne čelo vlny, stáva sa toto miesto podľa Huygensovho princípu novým zdrojom guľovej vlny.

            Za časový interval Dt guľová vlnoplocha, vychádzajúca z bodu A, postúpi do vzdialenosti v₂.Dt. Platí

 

                                                                                                (5.2.8.1)                                                                                                                               

                                                                                                              (5.2.8.2)

 

Podiel je

 

                                                                                                                 (5.2.8.3)

 

 

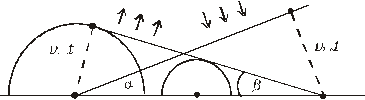
Tento vzťah vyjadruje známy zákon lomu, ktorý platí aj pre iné druhy vlnenia než len mechanické. Guľové vlny sa však šíria z rozhrania aj do prvého prostredia. Dostávame odrazenú vlnu.

 

 

                                                                       Obr. 5.2.8.3

 

 

            Pre odrazenú vlnu platí (Obr. 5.2.8.3) b = a, čiže uhol odrazu rovná sa uhlu dopadu.Toto tvrdenie je známe pod názvom zákon odrazu.

Existuje teda vlna odrazená i vlna prechádzajúca do druhého prostredia. Energia nesená dopadajúcou vlnou sa pritom rozdelí na energiu, odpovedajúcu odrazenej a prechádzajúcej vlne.

 

 

Príklad 5.2.4.  Pod akým najväčším uhlom môže dopadať zvuková vlna zo vzduchu na rozhranie vzduchu a vody,aby práve prestala prechádzať do druhého prostredia ?

Riešenie :   Ak veličiny pre prvé prostredie (vzduch) označíme indexom 1 a podobne veličiny pre druhé prostredie (vodu) indexom 2, potom zo vzťahu ( 5.2.8.3) vidíme, že narastanie čitateľa na ľavej strane (a teda i uhlu dopadu) tejto rovnice znamená súčasne narstanie menovateľa (teda aj uhlu lomu), lebo podiel je konštantný a rovná sa podielu rýchlostí šírenia vĺn v prvom a druhom prostredí. Hraničný prípad nastane vtedy,keď uhol a₂ je práve rovný p/2 ,vtedy práve vlnenie do druhého prostredia už nevstupuje. Máme teda

 

     

 

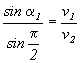
teda

  

 

z toho hraničný uhol je   a₁ = 13^o 33 ^´ .

 

 

 

Kontrolné otázky k časti  5.2.8

1.     Čo hovorí Huygensov princíp ?

2.     Ako zostrojíme novú vlnoplochu pomocou Huygensovho princípu ?

3.     Pomocou Huygensovho princípu vysvetlite odraz vĺn na rovinnom rozhraní dvoch homogénnych prostredí!

4.     Pomocou Huygensovho princípu vysvetlite lom vlny pri prechode takýmto rozhraním !

5.     Čo hovorí zákon lomu pre prechod vlny rovinným rozhraním ?

6.     Čo hovorí zákon odrazu na rovinnom rozhraní medzi dvomi prostrediami ?