5.2.4 Vlny vo vzduchovom stĺpci.

 

 

 

                                                            

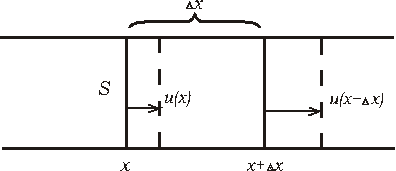
        Obr. 5.2.4.1

 

Predstavme si situáciu, keď je plyn (vzduch) uzavretý vo válci všade rovnakého prierezu S. Plyn vo valci je vlastne ďalší prípad pružného prostredia, preto na základe analógie s predchádzajúcimi odstavcami možno očakávať, že aj v tomto prípade môže nastať šírenie vĺn pozdĺž valca. Podobne jako predtým, os x orientujme v smere osi valca a výchylku v mieste x označíme u(x).

                                             

Objem uvažovaného elementu, daného intervalom (x, x+Dx)`pri posunutí bude

                                       (5.2.4.1)

 

Ak súčin S.Dx označíme V₀ (pôvodný objem elementu) máme

 

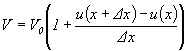                                                                                     (5.2.4.2)

 

Zmena objemu plynu je spojená so zmenou jeho tlaku. Pritom musíme vziať do úvahy, že procesy, spojené s kmitaním tlaku pri vlnových procesoch sú také rýchle, že sa pri nich nestačí vymieňať teplo medzi susednými elementami, ktoré pri stlačení nadobudli rôznu teplotu. Pri takýchto procesoch prebieha v plyne adiabatický proces

 

                                                                                                              (5.2.4.3)

 

kde c je Poissonova konštanta. Máme teda zo (5.2.4.2) po dosadení do (5.2.4.3) a vykrátení  V₀^χ

 

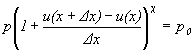                                                                                    (5.2.4.4)

 

a keď urobíme limitný prechod Dx® 0

 

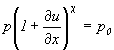                                                                                                        (5.2.4.5)

 

čiže

                                                                                                       (5.2.4.5)

 

Teraz urobíme podobnú úvahu, akú sme urobili s elementom pružnej tyče. V mieste x je tlak p(x), x-ová zložka sily pôsobiaca na element je p(x).S. V mieste x+Dx je x-ová zložka sily (sila pôsobí smerom doľava) –p(x+Dx).S. Celková sila pôsobiaca na element musí sa rovnať súčinu hmotnosti a zrýchlenia ťažiska elementu. Pre x-ové zložky teda máme

 

                                                                                (5.2.4.6)

 

z čoho podelením Dx a prechodom Dx®0

 

                                                                                                              (5.2.4.7)

 

Deriváciu tlaku podľa x urobíme zo vzťahu (5.2.4.5)

 

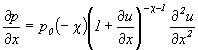                                                                                   (5.2.4.8)

 

Pretože sa zaoberáme len malými zmenami, hodnotu derivácie

 ,

 

ktorá má význam relatívnej deformácie (pozri vzťah (5.2.4.4),kde vznikla), budeme považovať za malú oproti jedničke,  a po dosadení do (5.2.4.7) máme

 

                                                                                                       (5.2.4.9)

Ak označíme

 

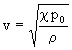                                                                                                                  (5.2.4.10)

 

opäť máme jednorozmernú vlnovú rovnicu

 

                                                                                                            (5.2.4.11)

 

Vo vzťahu (5.2.4.10) p₀ bol “ustálený tlak” plynu, ešte neovplynený vlnou. Ďalej ho budeme označovať už len p.

Veličiny vo vzťahu (5.2.4.10) určujúce rýchlosť šírenia sa vlny v plynnom stĺpci, vo všeobecnosti závisia od teploty.

 

Príklad 5.2.3.  Nájdite závislosť rýchlosti šírenia vĺn od teploty pre ideálny plyn. Ako sa zmení táto rýchlosť,keď absolútna teplota stúpne z hodnoty T_o = 300 K o 5% ?

Riešenie :   Na vyjadrenie hustoty použijeme stavovú rovnicu pre ideálny plyn

 

 kde M_mol  je hmotnosť jedného mólu ideálneho plynu. Hustota potom bude

 

 

 a po dosadení do (5.2.4.10) (za p_o už píšeme p)

 

 

 

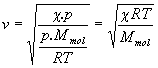
Pri zvýšení teploty z T_o o 5% bude  T=1,05 T_o,

 

       

 

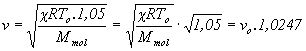
Rýchlosť sa teda zvýši o 2,47%.

 

 

 

Kontrolné otázky k časti  5.2.4

1.   Vysvetlite význam jednotlivých členov v rovnici (5.2.4.6) !

2.   Prečo uvažujeme proces v plyne ako adiabatický ?

3.   Od čoho závisí rýchlosť šírenia vlny v plyne ?