5.2.7 Prenos energie mechanickými vlnami

 

            Pri šírení mechanickej vlny sú častice prostredia v pohybe, majú teda určitú kinetickú energiu. Prostredie je súčasne nositeľom mechanickej deformácie a tým i určitej potenciálnej energie. Pri postupe vlny sa lokalizácia energie tiež mení, energia je nesená vlnou v smere jej postupu.

Uvažujme prenos energie pri šírení vlny pružným prostredím. Vezmime pre určitosť pružnú tyč s prierezom S, ktorou sa šíri pozdĺžna vlna.

 

 

 

 

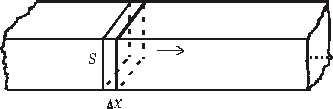
                                                                                 Obr. 5.2.7.1

 

Hustota kinetickej energie je

 

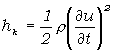                                                                                                        (5.2.7.1)

 

hustota potenciálnej energie, spojenej s relatívnou deformáciou e je

 

                                                                                                              (5.2.7.2)

 

kde za e môžeme dosadiť podľa (5.2.3.6)

 

                                                                                                                       (5.2.7.3)

 

V elemente objemu S.Dx je teda energia

 

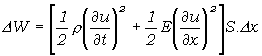                                                                   (5.2.7.4)

 

Ak výchylku postupujúcej vlny vyjadríme podľa vzťahu (5.2.2.8)

 

                                                                                                             (5.2.7.5)

 

vidíme, že platí

 

                                                                                                            (5.2.7.6)

 

 

(pozri vzťah (5.2.2.14)).

 

Ak pomocou posledného vzťahu v  rovnici (5.2.7.4) vylúčime

  ,

 

dostaneme

 

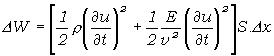                                                                (5.2.7.7)

 

Pretože je E/v² = r, máme

 

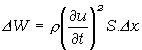                                                                                                 (5.2.7.8)

 

Táto energia sa dostala do uvažovaného elementu objemu spolu s vlnou tak, že za časový interval Dt prešla daným prierezom a vyplnila pritom element objemu šírky Dt. Delením DW súčinom S.Dt dostaneme, koľko energie prejde za jednotku času jednotkou plochy, čiže hustotu toku energie

 

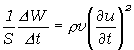                                                                                                   (5.2.7.9)

 

Vezmime teraz rovinnú harmonickú vlnu

 

                                                                                             (5.2.7.10)

 

Derivovaním a dosadením do (5.2.7.9) máme

 

                                                                           (5.2.7.11)

 

Okamžitá hodnota tohoto výrazu je daná funkciou cos²(kx-w t+j). Táto osciluje medzi nulou a jedničkou.

 

 

 

 

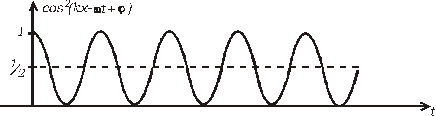
                                                                                   Obr. 5.2.7.2

 

 

Nás však zaujíma skôr stredná, priemerná hodnota výrazu (5.2.7.11). Tú dostaneme, ak za cos²(kx-wt+j) dosadíme jeho strednú hodnotu, rovnú 1/2.

Pre strednú hustotu toku energie teda máme

 

                                                                                          (5.2.7.12)

 

Túto veličinu nazývame intenzitou vlny. Je to teda množstvo energie, ktoré za jednotku času prejde jednotkou plochy, postavenou kolmo na smer šírenia. Z posledného vzťahu je vidieť, že je úmerná štvorcu amplitúdy mechanickej vlny.

Pri šírení guľovej vlny malé časti vlnoplochy sú prakticky rovinné, takže možno použiť vzťah (5.2.7.12). Rovnako veľká energia postupne prechádza cez guľové plochy, ktorých plošný obsah je úmerný štvorcu ich polomeru. Preto podľa posledného vzťahu A² musí byť úmerné 1/r², teda amplitúda vlny A je úmerná 1/r, čiže s narastajúcou vzdialenosťou od zdroja sa postupne zmenšuje.

Vo všeobecnosti riešením trojrozmernej vlnovej rovnice (5.2.6.9) je aj guľová vlna typu

 

                                                                                                   (5.2.7.13)

 

kde f(  ) je ľubovoľná funkcia, o čom sa možno presvedčiť priamo dosadením do uvedenej rovnice.

 

 

 

Príklad 5.2.4.  Aká je amplitúda výchylky vlny v kovovej tyči s hustotou  8000 kg.m ^–3 a rýchlosťou šírenia vlny v = 5000 m.s ^–1 , pri frekvencii  f = 20 kHz, keď intenzita vlny je  I = 10³ W.m^{-2  ?}

Riešenie :   Podľa vzťahu ( 5.2.7.12) máme

 

      ,  

 

 

A=5,63.10 ^–8 m

 

Vidíme, že amplitúda výchylky je i pri tejto intenzite pomerne malá.

 

 

 

Kontrolné otázky k časti  5.2.7

1.   Aké druhy energie nesie mechanická vlna ?

2.   Od čoho závisí hustota jej kinetickej energie ?

3.   Od čoho závisí hustota jej potenciálnej energie?

4.   Čo je intenzita vlny ? Od čoho závisí?

5.   Prečo amplitúda rozbiehavej guľovej vlny klesá s narastajúcim polomerom guľovej vlnoplochy ?