5.2.5. Harmonické vlny

 

Ako sme videli, vlny šíriace sa v smere osi x boli popísané vzťahom

 

                                                                                                    (5.2.5.1)

 

kde ľubovoľná funkcia f(  ) určovala vlastne tvar vlny. Špeciálnym prípadom je prípad, keď funkcia f(  ) je harmonická funkcia

 

                                                                                                (5.2.5.2)

 

 

Počiatočné rozloženie výchyliek je potom  periodické s amplitúdou A – pozri obr.(5.2.5.1).

 

 

 

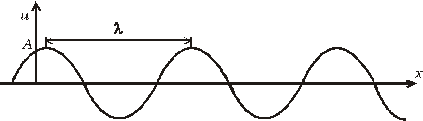
                                                                                     Obr. 5.2.5.1

 

Koeficient k súvisí s priestorovom periódou λ, ktorú nájdeme z podmienky: ak x zväčšíme o λ, argument funkcie sínus v (5.2.5.2) sa musí zväčšiť o 2p, čiže,

 

                                                                                                                      (5.2.5.3)

 

teda

                                                                                                                        (5.2.5.4)

 

Dĺžku λ  nazývame vlnová dĺžka danej vlny.

Obyčajne sa definuje vektor, ktorý má veľkosť podľa (5.2.5.4) a jeho smer je totožný so smerom šírenia vlny. Nazýva sa vlnový vektor (novší názov: uhlový vlnový vektor).

 

                                                                                                                      (5.2.5.5)

 

 

V čase t je celé rozloženie výchyliek posunuté o hodnotu v.t                                                           

 

                                                                                   (5.2.5.6)

 

čiže

                                                                                   (5.2.5.7)

 

 

 

               

                                                                                               Obr. 5.2.5.2

 

            Pozorovateľ, stojaci v mieste x, pozoruje časovú závislosť výchylky podľa vzťahu (5.2.5.7), teda ako periodickú s časom. Ak označíme najmenšiu časovú periódu ako T, potom zväčšenie t o hodnotu T musí znamenať prírastok argumentu vo vzťahu (5.2.5.7) o hodnotu

 

                                                                                                                  (5.2.5.8)

 

a ak za hodnotu k vezmeme podľa  (5.2.5.5)  2p ¤l, dostaneme        

 

                                                                                                                          (5.2.5.9)

 

čiže perióda sa súčasne rovná veľkosti časového intervalu, za ktorý vlna ubehne vzdialenosť rovnú jednej vlnovej dĺžke. Prevrátená hodnota periódy je frekvencia vlny

 

                                                                                                                        (5.2.5.10)

 

Uhlová frekvencia ω potom je

 

                                                                                                 (5.2.5.11)

 

Vzťah (5.2.5.7) potom možno vyjadriť

 

                                                                                    (5.2.5.12)

 

Nakoniec ešte uveďme, že j v tomto vzťahu nazývame fázový posun.

 

Kontrolné otázky k časti  5.2.5

1.     Aké je priestorové rozloženie výchyliek v harmonickej vlne ?

2.     Aký časový priebeh výchylky pozorujeme v jednom bode, ak sa prostredím šíri harmonická vlna?

3.     Čo je vlnová dĺžka, ako súvisí s periódou ?

4.     Čo je uhlová frekvencia, ako súvisí s vlnovým vektorom ?