5.2.2 Šírenie vĺn na strune. Vlnová rovnica
Príklad
s lanom z predchádzajúceho paragrafu má svoje exaktné matematické
vyjadrenie v analýze úlohy, známej už dávno pod názvom problém šírenia vĺn
na strune.
Pod
strunou budeme rozumieť tenké ohybné hmotné vlákno s lineárnou hustotou s, ktoré je napínané silou, ktorej
veľkosť označíme P. Predpokladá sa,
že vďaka ideálnej ohybnosti struny sila P
je rovnaká v každom mieste (reze) deformovanej či nedeformovanej struny
(Poznamenajme, že reálne struny nie sú ideálne ohybné, z tohoto hľadiska
sú bližšie k ideálu gumové nite). Rovnovážnu polohu struny stotožníme
s osou x. Výchylku struny
v mieste x a v čase t označíme u(x,t). Pre sformulovanie rovníc uvažujme element struny dĺžky Dx medzi bodmi x
a x+Dt.
(Obr. 5.2.2.1)
Uhol medzi dotyčnicou
k strune v danom mieste a osou x
označíme a(x).
Kolmá
zložka sily, pôsobiacej na element struny sprava v mieste x+Dx
je Psina(x+Dx), v mieste x zľava pôsobí kolmá zložka -Psina. Pre malé uhly (také predpokladáme) môžeme
s dobrou presnosťou písať sina![]() tga .
tga .
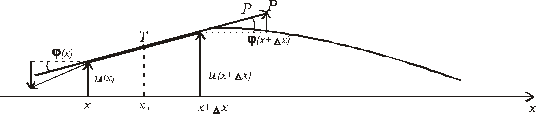
Obr. 5.2.2.1
Súčet
kolmých zložiek sily, ktorými pôsobí “okolie daného elementu” na tento element,
musí sa rovnať súčinu jeho hmotnosti s.Dx a zrýchlenia jeho ťažiska
![]() (5.2.2.1)
(5.2.2.1)
Delením šírkou intervalu Dx dostaneme
![]() (5.2.2.2)
(5.2.2.2)
Ak limitujeme Dx®0,
podiel na ľavej strane prejde na deriváciu
![]() (5.2.2.3)
(5.2.2.3)
Tu už nemusíme vyznačovať
ťažisko, pretože pri limitnom prechode pravý aj ľavý koniec, ako aj ťažisko, sa
dostanú do miesta x. Teraz ešte
uvážime, že tga
je vlastne smernica dotyčnice ku grafu funkcie u(x), platí teda
![]() (5.2.2.4)
(5.2.2.4)
Po dosadení tga do rovnice (5.2.2.3)
dostaneme
![]() (5.2.2.5)
(5.2.2.5)
Ak zavedieme označenie
![]() (5.2.2.6)
(5.2.2.6)
rovnica (5.2.2.5) prejde na tvar
![]() (5.2.2.7)
(5.2.2.7)
Táto rovnica,
ktorá je vlastne výsledkom aplikovania Newtonovej pohybovej rovnice na element
struny, sa v tomto tvare vyskytuje aj pri popise iných prípadov šírenia
vĺn (jednorozmerného), nazýva sa preto jednorozmernou vlnovou rovnicou.
Zdôrazníme,
že do úvahy sme nezahrnuli vonkajšie sily, t. j. sily, ktoré dajú strunu do pohybu, alebo sily trenia
v odporovom prostredí (vzduchu), ale len vnútorné sily v strune.
Rovnica (5.2.2.7) môže teda popisovať vlnové procesy pre prípad, že už nejaké
výchylky struny boli vytvorené. Pridaním budiacich síl by sme dostali tzv.
nehomogénnu vlnovú rovnicu, ktorou sa zatiaľ nebudeme zaoberať.
Už
z tvaru rovnice (5.2.2.7) je vidieť, že jej riešeniami sú fukcie (aspoň)
dvoch premenných, x a t,
u(x,t), teda výchylka v mieste
x vo všeobecnosti závisí
ešte od času t.
Ukážme
teraz, že riešením rovnice (5.2.2.7) je funkcia, ktorá má tvar, odpovedajúci
postupujúcej vlne, o ktorej sme hovorili v úvode tejto časti, t. j. tvar
u = f (x – v.t) , (5.2.2.8)
kde f( ) je ľubovoľná (dvakrát
derivovateľná) funkcia.
Overme si, že
uvedená funkcia je naozaj riešením rovnice (5.2.2.7). Vytvoríme derivácie,
ktoré potrebujeme . Označme preto argument x-vt
jako s
s = x – vt . (5.2.2.9)
Potom
![]() (5.2.2.10)
(5.2.2.10)
a pre druhú deriváciu podobne
![]() (5.2.2.11)
(5.2.2.11)
Pri derivácii podľa času máme
![]() (5.2.2.12)
(5.2.2.12)
ale pretože
![]() (5.2.2.13)
(5.2.2.13)
máme
![]() (5.2.2.14)
(5.2.2.14)
a opakovaním
![]() (5.2.2.15)
(5.2.2.15)
Vidíme, že (5.2.2.7)
skutočne je splnené
![]() (5.2.2.16)
(5.2.2.16)
a to bez ohľadu na to, aká je
konkrétna funkcia f(x-v.t), stačí, že
má druhé derivácie. Význam tohoto je jednoduchý. V čase t = 0 je
výchylka podľa (5.2.2.8)
u(x,0) = f(x), (5.2.2.17)
čiže funkcia f(x) určuje konkrétne rozloženie výchyliek v čase t=0, čiže “TVAR VLNY” a ako sme videli
v úvode tejto časti, v ďalšom sa výchylka posúva, v čase t je rozloženie posunuté o hodnotu v.t, čomu odpovedá “posunutá” funkcia f(x-vt).
Pretože
fyzikálne smer osi +x je rovnocenný
so smerom opačným, je rozumné očakávať, že rovnica (5.2.2.7) pripúšťa aj
riešenie popisujúce vlny, šíriace sa opačným smerom, t. j. v čase t posunutie bude (-vt)
![]() (5.2.2.18)
(5.2.2.18)
tu g( ) je opäť ľubovoľná
funkcia (jedného argumentu), ktorá je dvakrát derivovateľná.
![]()
Príklad
5.2.1. Je potrebné rozlišovať rýchlosť postupu vlny
a okamžitú rýchlosť vt bodu na strune. Vyjadrite vzťah medzi
týmito veličinami !
Riešenie : Pre funkciu
tvaru (5.2.2.8) máme s použitím označenia (5.2.2.9)
![]()
kde
posledná derivácia v tomto vzťahu má význam smernice dotyčnice
k strune v danom mieste. Ak napríklad dotyčnica k strune v danom
mieste zviera s osou x uhol 30o a smernica je kladná,je
![]()
Vidíme,
že uvedené rýchlosti sa (čo do veľkosti) rovnajú len keď uhol a je 45o.
![]()
Princíp superpozície.
Tvar vlnovej
rovnice zaručuje, že ak máme dve možné rozloženia výchyliek u1(x,t) a u2(x,t) (t. j. dve vlny) vyhovujúce
rovnici (5.2.2.7)
![]() (5.2.2.19)
(5.2.2.19)
![]() (5.2.2.20)
(5.2.2.20)
potom sčítaním týchto rovníc
dostaneme
![]() (5.2.2.21)
(5.2.2.21)
to znamená, že vlna popísaná u(x,t), ktorú dostaneme sčítaním číže
superpozíciou vĺn u1(x,t) a u2(x,t), je tiež riešením vlnovej rovnice, čiže môže
reálne existovať.
Sčítaním
funkcií popisujúcich priamu a spätnú vlnu
![]() (5.2.2.22)
(5.2.2.22)
vzhľadom na ľubovoľnosť funkcií f(..) a g(..) dostávame všeobecné riešenie rovnice (5.2.2.7). Teda každý prípustný
vlnový stav v ľubovoľnom intervale možno popísať ako superpozíciu priamej
a spätnej vlny určitého tvaru.
Superpozíciu možno dobre ilustrovať sčítaním priamej a spätnej vlny, ktoré boli najprv priestorovo oddelené a postupne sa dostali do spoločnej oblasti – pozri Obr. 5.2.2.2.
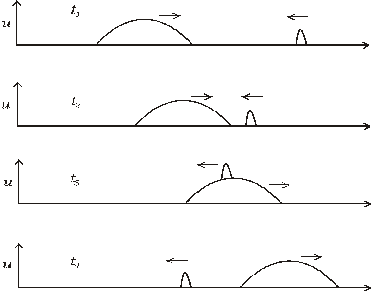
Obr.5.2.2.2
Je vidieť, že každá zo zúčastnených vĺn je po ich priestorovom oddelení taká, ako keby sa prostredím šírila samostatne, t.j. vlny sa v tomto zmysle vzájomne neovplyvňujú.Táto vlastnosť je charakteristická aj pre iné druhy vĺn, pokiaľ je prostredie, v ktorom sa vlny šíria také, že pripúšťa ich popis lineárnymi diferenciálnymi rovnicami.
Kontrolné otázky k časti 5.2.2
1. Vysvetlite význam jednotlivých členov v rovnici (5.2.2.1) !
2. Ktoré sily sme pri odvodzovaní rovnice
(5.2.2.1) nevzali do úvahy ?
3. Interpretujte riešenie (5.2.2.8) !
4. Interpretujte riešenie (5.2.2.18) !
5. Čo hovorí princíp superpozície vĺn ?
6. Aké je všeobecné riešenie vlnovej rovnice (5.2.2.7) ?
7. Od ktorých veličín charakterizujúcich strunu
závisí rýchlosť šírenia vĺn ?