6.4.3 Energia sústavy nábojov

Jednoduchými pokusmi sa môžeme presvedčiť, že elektrostatické pole má svoju energiu, ktorá vyjadruje schopnosť konať prácu na úkor zmeny tohoto poľa. Ak dosky nabitého kondenzátora spojíme vodičom, potom elektrický prúd vyvinie na vodiči teplo, ktorého veľkosť priamo súvisí so zmenou napätia na kondenzátore.

Úbytok energie elektrického poľa preto môžeme vyjadriť pomocou práce, ktorú toto pole vykoná. Opačne veľkosť energie poľa sa dá vypočítať ako práca vonkajších síl, ktoré daná pole premiestnením náboja vytvoria.

V časti 6.1.10 sme vyjadrili prácu pri premiestňovaní náboja v elektrickom poli. Energia náboja Q v danom mieste elektrického poľa sa rovná sa práci, ktorú musia vykonať vonkajšie sily pri premiestnení náboja do daného miesta zo zvoleného vzťažného bodu. Vzťažný bod sme volili v nekonečne, kde sila elektrického poľa je nulová. Vytvorme elektrické pole E₂ bodovým nábojom Q₂ a premiestňujme v jeho poli náboj Q₁ do bodu 1.  Potom táto práca sa dá vyjadriť:

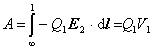 ,                                                                                          (6.4.5)
kde vonkajšia sila je opačná k elektrickej sile Q₁E₂, a V₁ je potenciál elektrického poľa vytvorený nábojom Q₂ v bode 1.

Celú situáciu môžeme vytvoriť i opačným postupom. Do poľa vytvoreného nábojom Q₁ vkladajme náboj Q₂ do miesta 2, tak že postavenie nábojov bude rovnaké, potom aj práca bude rovnaká o čom sa môžeme presvedčiť zo vzťahu pre potenciál bodového náboja (6.1.19).Takže môžeme napísať elektrostatickú energiu dvoch bodových nábojov i v symetrickej forme:

 ,              

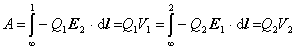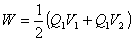
Posledný vzťah sa dá i zovšeobecniť pre sústavu bodových nábojov. Energia elektrického poľa sústavy nábojov je daná vzťahom:

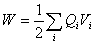,                                                                                                         (6.4.6)
kde V_i , je potenciál (vzhľadom na nekonečno) sústavy všetkých nábojov okrem náboja Q_i