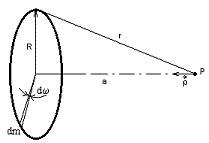
121. Vypočítajte potenciál a intenzitu gravitačného poľa drôtu hmotnosti m, ohnutého do tvaru kružnice s polomerom R v bode P na osi kružnice vo vzdialenosti a od jej stredu (obr.)!

      Kružnicu s polomerom R si môžeme rozdeliť na jednotlivé elementy, pričom každý element hmotnosti dm má od bodu P rovnakú vzdialenosť r, ktorú vypočítame podľa Pytagorovej vety:

(1)

Každému elementu s hmotnosťou dm prislúcha element obvodu kružnice do, pre ktorý platí:

(2)

kde ω je z intervalu <0, 2π>. Pre veľkosť elementu hmotnosti dm môžeme teda písať:

(3)

kde O predstavuje obvod drôtu (kružnice) (O = 2πR). Element drôtu dm, vybraný v podobe úseku drôtu dĺžky do prispieva k celkovému potenciálu φ v bode P hodnotou:

dφ = - κ / r  dm  

(4)

(5)

Celkový potenciál gravitačného poľa drôtu φ v bode P dostaneme integrovaním cez celý obvod kružnice:

φ = - κ [m / (2πR)] / ( R² + a² )^1/2  ∫_o^2πR  do  

         φ  = - κ  [(m / 2πR) / ( R² + a² )^1/2]  2πR

(6)

Potenciál gravitačného poľa drôtu je φ  = - κ m / ( R² + a² )^1/2.

Medzi vektorom intenzity K a potenciálom φ v ľubovoľnom mieste gravitačného poľa platí vzťah:

(7)

kde grad φ predstavuje zmenu potenciálu v smere a:

(8)

Zderivovaním a úpravou predchádzajúcich vzťahov dostávame:

  K = [- κ m ( R² + a² )^-1/2 ] ^' ρ

  K = κ m / 2 ( R² + a² )^-3/2 2a ρ

K = κ ma ( R² + a² )^-3/2 ρ

(9)

Intenzita gravitačného poľa drôtu je K = κ ma ( R² + a² )^-3/2 ρ .

Entropia ideálneho plynu