|

|
|
9. Cyklista sa pohybuje
smerom do kopca rýchlosťou v1
= 10 km.h-1. Keď dosiahne
vrchol kopca, obráti sa a absolvuje tú istú trasu z kopca dolu rýchlosťou
v2 = 40 km.h-1.
Aká bola priemerná rýchlosť cyklistu ?
|
|
| |
|
|
|
|
|
|
|
|
v1
= 10 km.h-1
v2
= 40 km.h-1
vp
= ?
|
|
|
 |
| |
|
|
|
| |
|
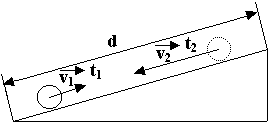
Pohyb do kopca a z kopca
môžme považovať za rovnomerný priamočiary. Vzdialenosť medzi zemou a
vrcholom kopca si označme d. Pri pohybe do kopca prejde
cyklista dráhu:
|
|
| |
|
|
d
= v1t1 .
|
(1)
|
|
| |
|
Pri pohybe z
kopca prejde tú istú dráhu za čas t2 rýchlosťou
v2, čiže:
|
|
| |
|
|
d
= v2t2 ,
|
(2)
|
|
| |
|
kde t1 je čas
výstupu a t2 čas zostupu. Priemerná rýchlosť
vp je definovaná ako celková prejdená dráha
s za celkový čas t. Môžme písať:
|
|
| |
|
|
vp
= s / t .
|
(3)
|
|
| |
|
Platí, že cyklista prejde celkovú dráhu:
|
|
| |
|
|
s
= 2d
|
(4)
|
|
| |
|
za čas
|
|
| |
|
|
t
= t1 + t2 .
|
(5)
|
|
| |
|
Po dosadení do vzťahu (3) za
priemernú rýchlosť vp dostaneme:
|
|
| |
|
|
vp
= s / t
vp
= 2d / (t1 + t2)
t1
= d / v1
t2
= d / v2
vp
= 2d / (d / v1 + d / v2)
vp
= 2d / (d (v1 + v2) / v1v2)
vp
= 2v1v2 / (v1 + v2)
|
|
|
| |
|
Dosadením
zadaných hodnôt dostávame:
|
|
| |
|
vp
= 2 . (400 / 50) km.h-1 = 16 km.h-1
.
|
|
| |
|
|
|
| |
|
Cyklista
sa pohybuje priemernou rýchlosťou 16 km.h-1. |
|
| |
|
|
|
| |
|
 Odraz
guľôčky Odraz
guľôčky
 Balistické
kyvadlo Balistické
kyvadlo
 Koeficient
tlmenia Koeficient
tlmenia
|
|
| |
|
|
|
 |
|

|
 |