


Chyby merania - Teória
- Teoretický úvod
- Štatistické spracovanie nameraných výsledkov
- Praktický postup pri meraniach
- Vyhodnotenie nepriameho merania
Praktický
postup pri meraniach
Ciele každého merania môžeme rozložiť na:
- čo najviac sa priblížiť
k správnej hodnote
 meranej fyzikálnej veličiny X
meranej fyzikálnej veličiny X - pre požadovanú mieru spoľahlivosti P určiť interval spoľahlivosti merania
Je zrejmé, že
v pri realizácii merania nemôžeme dosiahnuť nekonečný počet meraní pre
určenie hodnôt ![]() a
a
![]() . S použitím štatistiky
môžeme však tieto hodnoty určiť s obmedzenou presnosťou so súboru pozostávajúceho
z konečného počtu meraní.
. S použitím štatistiky
môžeme však tieto hodnoty určiť s obmedzenou presnosťou so súboru pozostávajúceho
z konečného počtu meraní.
Ak meraním fyzikálnej veličiny získame súbor nameraných hodnôt
Xi, i=1,...,n potom hodnote ![]() sa použitím tohoto súboru najviac blíži hodnota, ktorú nazývame aritmetický
priemer, označíme ju Xn a vypočítame ju pomocou
vzťahu:
sa použitím tohoto súboru najviac blíži hodnota, ktorú nazývame aritmetický
priemer, označíme ju Xn a vypočítame ju pomocou
vzťahu:
Rozptyl merania chrakterizuje stredná kvadratická ochýlka merania. Tú určíme pomocou vzťahu:
Hodnoty Xn a
![]() závisia od konkrétneho
súboru nameraných hodnôt a majú teda tiež náhodný charakter. Keby sme
merali veľa takýchto súborov, pre každý určili túto dvojicu hodnôt, potom
možno dokázať, že platí:
závisia od konkrétneho
súboru nameraných hodnôt a majú teda tiež náhodný charakter. Keby sme
merali veľa takýchto súborov, pre každý určili túto dvojicu hodnôt, potom
možno dokázať, že platí:
kde symbol <.>znamená strednú hodnotu. Vzhľadom na vzťah je účelné zaviesť štandardnú odchýlku merania vzťahom
pre ktorú platí
vzhľadom na vzťah (6) a (7) .![]()
Ak použijeme najpravdepodobnejšiu hodnotu Xn ako výsledok
merania, zaujíma nás, ako presne táto hodnota vystihuje správnu hodnotu
X. Keďže Xn je tiež náhodnou veličinou,
zaujíma nás jej disperzia.
Možno dokázať, že ak pre meranie veličiny x platí normálne
rozdelenie s disperziou ![]() ,
potom pre hodnoty Xn platí tiež normálne rozdelenie,
ale s n-krát menšou disperziou, takže stredná
kvadratická chyba aritmetického priemeru je určená vzťahom:
,
potom pre hodnoty Xn platí tiež normálne rozdelenie,
ale s n-krát menšou disperziou, takže stredná
kvadratická chyba aritmetického priemeru je určená vzťahom:
Aritmetický priemer
tak oveľa lepšie vystihuje správnu hodnotu ako jednotlivé merania.
Interval spoľahlivosti (resp. náhodnú chybu merania) určíme pre požadovanú
spoľahlivosť P podľa vzťahu (4) s tým,
že namiesto ![]() použijeme
použijeme
![]() .
.
Pri reálnom meraní na laboratórnych cvičeniach však nemôžeme získať veľké
množstvo opakovaných súborov (najmä kvôli časovej náročnosti). Uspokojíme
sa teda s jedným súborom.
Z toho dôvodu nemôžeme určiť stedné hodnoty (7) a (8).
Vo vzťahu (10) použijeme namiesto strednej hodnoty štandardnej
odchýlky hodnotu získanú z jediného súboru, takže
s tým, že veličinu
![]() stanovujeme s obmedzenou
presnosťou, ktorá súvisí s disperziou štandardnej odchýlky
stanovujeme s obmedzenou
presnosťou, ktorá súvisí s disperziou štandardnej odchýlky
Relatívna presnosť
hodnoty ![]() stanovenej
podľa (11) odpovedá podľa (12) hodnote
stanovenej
podľa (11) odpovedá podľa (12) hodnote
![]() , čo napríklad
pre n = 10 znamená 24%, pre n = 50 10%.
, čo napríklad
pre n = 10 znamená 24%, pre n = 50 10%.
Z toho vyplýva, že pri bežných počtoch opakovaných meraní n
< 100 má zmysel udávať chybu iba na jedno desatinné miesto.
Nakoľko ![]() stanovená
podľa (11) je priaznivejšia (menšia) ako správna hodnota
podľa (10), musíme túto skutočnosť rešpektovať pri určovaní
intervalu spoľahlivosti (resp. náhodnej chyby merania).
stanovená
podľa (11) je priaznivejšia (menšia) ako správna hodnota
podľa (10), musíme túto skutočnosť rešpektovať pri určovaní
intervalu spoľahlivosti (resp. náhodnej chyby merania).
Pre danú mieru spoľahlivosti P a pre daný počet meraní
n určíme pološírku
intervalu spoľahlivosti zo vzťahu
kde tp;n sa nazýva Studentov koeficient. Okrem normálneho rozdelenia rešpektuje aj konečný počet meraní.
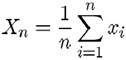 (5
(5 (6
(6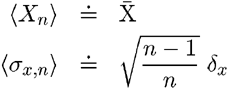 (7),(8)
(7),(8) (9
(9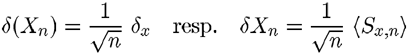 (10)
(10)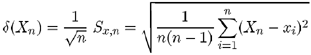 (11)
(11)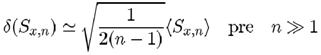 (12)
(12)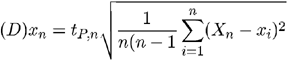 (13)
(13)