


Chyby merania - Teória
- Teoretický úvod
- Štatistické spracovanie nameraných výsledkov
- Praktický postup pri meraniach
- Vyhodnotenie nepriameho merania
Štatistické
spracovanie nameraných výsledkov
Nech x
je fyzikálna veličina a n nech je počet jej meraní. S
týchto hodnôt zostrojíme histogram (Obr.). Ten znázorňuje početnosť získaných
výsledkov. Os x predstavuje hodnoty meranej veličiny
x. Tú rozdelíme na malé intervaly a nad každým intervalom
zostrojíme obdĺžnik o výške rovnej relatívnej početnosti výskytu výsledkov
z daného intervalu. Je zrejmé, že skutočná hodnota meranej veličiny sa
nachádza v blízkosti maxima histogramu, pričom pravdepodobnosť výskytu
značne odlišných výsledkov rýchle klesá.
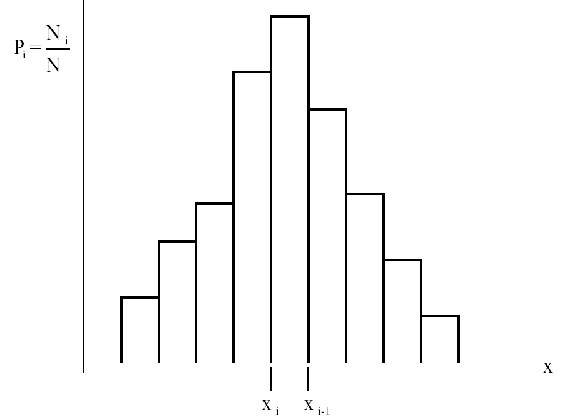
Obr. 1: Histogram zostavený z nameraných hodnôt veličniy x
Pri zväčšovaní počtu meraní n sa spresňuje informácia
o hodnote meranej veličiny.
Ak "zalimitíme" ![]() ,
dostaneme namiesto histogramu spojitú krivku, nazývame ju hustota
pravdepodobnosti rozdelenia f(x). Integráciou funkcie f(x)
v rozsahu od x1 po x2 dostávame pravdepodobnosť
toho, že meraná veličina bude ležať v intervale <x1; x2>.
,
dostaneme namiesto histogramu spojitú krivku, nazývame ju hustota
pravdepodobnosti rozdelenia f(x). Integráciou funkcie f(x)
v rozsahu od x1 po x2 dostávame pravdepodobnosť
toho, že meraná veličina bude ležať v intervale <x1; x2>.
Väčšina merania odpovedá Gaussovemu normálnemu rozdeleniu pravdepodobnosti.
Pre merania vtedy platí:
- výsledky merania môžu nadobúdať spojité spektrum hodnôt
- pri vysokom počte meraní majú chyby opačného znamienka rovnakú pravdepodobnosť
- s rastom chyby klesá pravdepodobnosť jej výskytu
Funkcia hustoty pravdepodobnosti normálneho rozdelenia má tvar:
je stredná hodnota veličiny x a reprezentuje (správnu)
hodnotu veličiny X a
je disperzia (rozptyl) meranej veličiny a súvisí so šírkou rozdeľovacej
funkcie. Veličina ![]() je
je
stredná kvadratická chyba a udáva, ako sú rozptýlené
merané hodnoty veličiny okolo strednej
hodnoty ![]() . Ak vymedzíme
interval
. Ak vymedzíme
interval ![]() , potom
veličina P(Dx) vyjadruje
, potom
veličina P(Dx) vyjadruje
pravdepodobnosť, že náhodná veličina padne do tohoto intervalu. Veličina
P sa nazýva miera
spoľahlivosti (udáva sa ako číslo z intervalu <0; 1> alebo
v %), príslušný interval sa nazýva
interval spoľahlivosti a hodnota Dx predstavuje náhodnú
chybu merania pre danú mieru
spoľahlivosti.
Táto chyba súvisí s ![]() vzťahom:
vzťahom:
![]()
kde koeficient tp sa určí integráciou funkcie (1).
Keďže výpočet tohoto integrálu je pomerne
zložitý a zdĺhavý, pre praktické prípady možno nájsť hodnoty koeficientov
v tabuľkách.
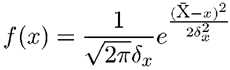 (1
(1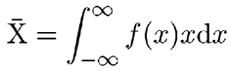 (2
(2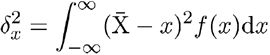 (3
(3