ŠTRUKTÚRA KVAPALÍN A ICH POVRCHOVÁ VRSTVA
Z výsledkov experimentov s kvapalinami vyplýva, že kvapaliny majú podobnú štruktúru ako amorfne latky. Častice v najbližšom okolí danej častice sú vzhľadom na ňu usporiadane približne pravidelne, no so zväčšovaním vzdialenosti sa táto pravidelnosť porušuje (pozri obr. 3-24b). Každá častica kmitá okolo svojej rovnovážnej polohy a po vekmi krátkom čase (radovo ns) sa premiesti a zaujme novú rovnovážnu polohu. Keď sa teplota kvapaliny zvyšuje, čas, za ktorý častica zotrváva v danej rovnovážnej polohe, sa zmenšuje.
Kvapaliny na rozdiel od plynov sa vyznačujú malými vzájomnými vzdialenosťami medzi molekulami (radovo 0,1 nm). Preto molekuly na seba pôsobia veľkými príťažlivými silami. Tieto sily majú vplyv najmä na vlastnosti voľného povrchu kvapaliny, ktorý tvorí rozhranie medzi kvapalinou a jej parou alebo iným plynom.
Vlastnosti povrchu kvapaliny vysvetlime z hľadiska molekulovej fyziky takto: Okolo každej molekuly kvapaliny si môžeme predstaviť guľu s takým polomerom rm, že príťažlivé sily, ktorými na túto vybranú molekulu pôsobia molekuly mimo guľu, sú zanedbateľné. Myslenú guľu, v ktorej na seba navzájom pôsobia molekuly kvapaliny, nazývame
sféra molekulového pôsobenia. Jej polomer rm je rádovo 1 nm.
Keď je sféra molekulového pôsobenia vnútri kvapaliny, potom sa príťažlivé sily, ktorými molekuly v tejto sfére pôsobia na uvažovanú molekulu, navzájom rušia (obr. 3-35, sféra
K1 a K2). V inej situácii sú molekuly, ktorých vzdialenosť od voľného povrchu kvapaliny je menšia ako rm .Ich sféry molekulového pôsobenia zasahujú do ďalšieho prostredia (obr. 3-35, sféry
K3 a K4). Výslednica F príťažlivých síl, ktorými pôsobia molekuly kvapaliny v spodnej časti sfér
K3 a K4
na molekuly v ich stredoch, je kolmá na voľný povrch kvapaliny a ma smer dovnútra kvapaliny. Molekuly pary kvapaliny a plynov nad kvapalinou v hornej časti sfér
K3 a K4
pôsobia na uvažované molekuly výslednou príťažlivou silou F', ktorá má opačný smer ako sila F. Vo väčšine prípadov je hustota častíc v týchto horných sférach oveľa menšia ako hustota molekúl v dolných sférach, preto F' < < F a silu F' môžeme zanedbať.
Vrstva molekúl, ktoré majú od voľného povrchu kvapaliny menšiu vzdialenosť ako je polomer sféry molekulového pôsobenia, nazýva sa povrchová vrstva kvapaliny.
Na každú molekulu. ktorá leží v povrchovej vrstve kvapaliny, pôsobia susedné molekuly výslednou príťažlivou silou so smerom dovnútra kvapaliny.
Spomenutá vlastnosť povrchovej vrstvy spôsobuje, že voľný povrch kvapaliny sa správa podobne ako tenká pružná blana. Svedčia o tom napr. tieto javy: Keď na voľný povrch vody položíme ihlu alebo žiletku, povrch vody sa prehne a predmety sa nepotopia, hoci hustota látky, z ktorej sú zhotovené, je väčšia ako hustota vody. Kvapka, ktorá sa tvorí na konci nie je celkom uzavretého vodovodného kohútika, postupne rastie, potom sa uzatvorí zúžené hrdlo a kvapka sa odtrhne.
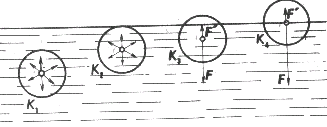
Obr. 3-35 Znázornenie príťažlivého pôsobenia molekúl vo sfére molekulového pôsobenia
POVRCHOVÁ ENERGIA A POVRCHOVÉ NAPÄTIE
Na posunutie molekuly z vnútra kvapaliny do jej povrchovej vrstvy treba vykonať prácu. Preto molekuly povrchovej vrstvy majú väčšiu potenciálnu energiu vzhľadom na susedné molekuly, ako by mali, keby boli vnútri kvapaliny.
Rozdiel medzi potenciálnou energiou, ktorú majú molekuly v jej povrchovej vrstve a potenciálnou energiou, ktorú by mali tie isté molekuly vnútri kvapaliny vzhľadom na susedné molekuly, sa volá povrchová energie
E kvapaliny.
Zväčšením voľného povrchu kvapaliny sa jej povrchová energie zväčšuje. Zmena povrchovej energie
∆E je priamo úmerná zmene obsahu ∆S voľného povrchu kvapaliny
∆E
= σ∆S
(3.29)
Konštanta úmernosti sa volá povrchové napätie. Závisí od druhu kvapaliny a prostredia nad voľným povrchom kvapaliny. So zvyšujúcou teplotou povrchové napätie klesá. Zo vzťahu (3.29) vyplýva, že jednotkou povrchového napátia je newton na meter
(N.m-1).
Kvapalina s daným objemom nadobúda vždy taký tvar, aby obsah povrchu bol čo najmenší. Pri danom objeme má zo všetkých telies najmenší obsah povrchu guľa. Preto napr. voľné kvapky hmly alebo rosy majú guľový tvar.
Keď je kvapka dosť veľká, deformuje jej guľový tvar tiažová sila. Ak túto silu vykompenzujeme napr. vztlakovou silou, nadobúdajú guľový tvar aj väčšie kvapky.
Povrchové napätie definované z energetického hľadiska vzťahom (3.29) môžeme zaviesť ešte iným spôsobom. Ukážeme to pokusom s mydlovým alebo saponátovým roztokom.
Na drôtenom rámčeku s jednou pohyblivou stranou utvoríme blanu z mydlového roztoku (obr. 3-36). Pozorujeme, že sa blana sťahuje a ťahá za sebou aj drôtik AB. To značí, že na drôtik AB pôsobí v rovine rámčeka sila
F kolmá na priečku AB. Túto silu, ktorú nazývame
povrchová sila, môžeme zmerať.
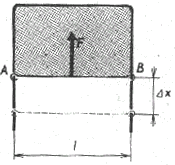
Obr. 3-36 Pôsobenie povrchovej sily mydlinovej blany na pohyblivú priečku AB
Keď pohyblivú priečku AB zaťažíme tak, aby sústava bola v rovnováhe, potom na priečku pôsobí tiaž G zvislo nadol a povrchová sila 2F (blana má dva povrchy) zvislo nahor, pričom G = 2F.
VeIkosť povrchovej sily je teda 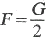
Ked' pôsobením vonkajšej sily zväčšíme (pri konštantnej teplote) povrch blany, prechádza časť
molekúl z vnútra kvapaliny na oba povrchy a povrchová energia blany sa zväčšuje. Práca W
vykonaná pôsobením vonkajších síl sa rovná prírastku povrchovej energie
∆E blany. Pri zmenšovaní
povrchu blany časť molekúl prechádza z oboch povrchových vrstiev dovnútra kvapaliny, povrchová
energia blany sa zväčšuje a blana koná prácu.
Posunutím priečky AB o dĺžku ∆x (obr. 3-36) sa zmení obsah o 2∆S = 2l ∆x a podľa vzťahu (3.29) zmena
povrchovej energie ∆E = 2σ ∆S
= 2σl ∆x,
kde l je dĺžka priečky. Keď prácu vyjadríme vzťahom W
= 2F ∆x, potom z rovnosti ∆E = W
vyplýva pre povrchové napätie vzťah
 (3.30)
(3.30)
Povrchové napätie sa rovná podielu povrchovej sily a dĺžky okraja povrchovej blany, na ktorý pôsobí sila kolmo v povrchu kvapaliny.
Vzťah (3.30) potvrdzuje, že jednotkou povrchového napátia je
N.m-1. Povrchové napätia niektorých kvapalín (v styku so vzduchom) pri danej teplote sú v MFChT. Napríklad pre vodu pri teplote 20 °C
σ = 73 mN-1 . m.

Obr. 3-37 Pokus na pôsobenie povrchových sil na okaj mydlinovej blany
Keď do čistej sklenej nádoby nalejeme vodu, pozorujeme, že pri stene nádoby je voľný povrch vody
dutý (obr. 3-38a). Dutý povrch tvorí aj lieh v sklenej nádobe alebo ortuť v medenej nádobe. V týchto prípadoch kvapalina steny nádoby
zmáča.
Keď do čistej sklenej nádoby nalejeme ortuť, je pri stene nádoby voľný povrch kvapaliny vypuklý (obr. 3-38b). Kvapalina steny nádoby
nezmáča.
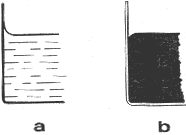
Obr.3-38 Zakrivenie volného povrchu kvapaliny
Zakrivenie voľného povrchu kvapaliny je spôsobené tým, že molekuly kvapaliny, ktoré sú na jej voľnom povrchu a súčasne v blízkostí steny nádoby iného pevného telesa, pôsobia navzájom nielen medzi sebou, ale aj s časticami pevného telena a plynu nad voľným povrchom kvapaliny. Ak výslednice tohto pôsobenia smeruje von z kvapaliny, tak voľný povrch kvapaliny pri stene nádoby je dutý. Ked' výslednica smeruje do vnútra kvapaliny, volný povrch kvapaliny pri stenách nádoby je vypuklý.
Zakrivenie voľného povrchu kvapaliny spôsobuje, že výslednicou povrchových síl je nenulová tlaková sila, ktorá pôsobí kolmo na voľný povrch kvapaliny. Na obr. 3-39 je táto situácia znázornená pre dutý a vypuklý povrch kvapaliny v úzkej trubici. Vzniknutá tlaková sila vyvoláva
kapilárny tlak.

Obr. 3-39 Znázornenie smeru tlakovej sily, ktorou zakrivený povrch pôsobí na kvapalinu
Možno odvodiť, že pre voľný povrch kvapaliny guľového tvaru je kapilárny tlak
pk daný vzťahom
 (3.30)
(3.30)
kde R je polomer guľového povrchu a σ povrchové napätie kvapaliny.
Závislosť kapilárneho tlaku od polomeru zakrivenia móžeme demonštrovať týmto pokusom: Na dvojramennej sklenej trubici s trojcestným kohútikom K (obr. 3-40) vyfúkneme postupne dve mydlinové bubliny s rozličnými polomermi. Keď otočením kohútika obe bubliny spojíme, pozorujeme, že bublina s väčším polomerom sa zväčšuje a bublina s menším polomerom sa zmenšuje, až zanikne. To značí, že v menšej bubline je väčší kapilárny tlak ako vo väčšej bubline.
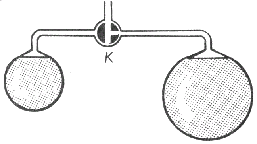
Obr. 3-40 Pokus na závislost' kapilárneho tlaku od polomeru mydlinovej bubliny
V dôsledku existencie kapilárneho tlaku pri kvapalinách so zakriveným povrchom pozorujeme zvýšenie alebo zníženie voľnej hladiny kvapaliny vo veľmi úzkych trubiciach -
kapilárach, ktoré sú na oboch koncoch otvorené a čiastočne zasunuté do kvapaliny v nádobe (obr. 3-41). Pri kvapalinách, ktoré zmáčajú steny kapiláry a majú tiež dutý povrch, pozorujeme zvýšenie voľnej hladiny kvapaliny v kapiláre (obr. 3-41a). Jav nazývame
kapilárna elevácia. Pri kvapalinách, ktoré nezmáčajú steny kapiláry (voľný povrch vypuklý), pozorujeme zníženie voľnej hladiny kvapaliny v kapiláre (obr. 3-41 b). Jav v tomto prípade nazývame kapilárna depresia. Javy kapilárnej depresie a elevácie súhrnne nazývame kapilaritou.
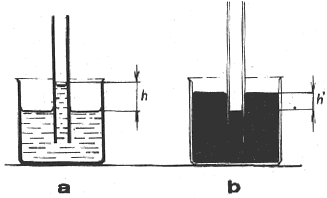
Obr. 3 - 41 Pokus na a) kapilárnu eleváciu, b) kapilárnu depresiu
na začiatok
|
