53. Hmotný bod koná pohyb po kružnici s polomerom R = 20 cm so stálym uhlovým zrýchlením ε = 2 s^-2. Vypočítajte hodnotu tangenciálneho, normálového a celkového zrýchlenia na konci štvrtej sekundy od začiatku pohybu, keď v čase t = 0 s bol hmotný bod v pokoji!

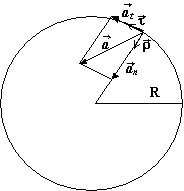
Pri pohybe po kružnici možno zrýchlenie hmotného bodu rozložiť na zložku tangenciálnu (dotyčnicovú) a_t a zložku normálovú (dostredivú) a_n, pričom platí:

a = a_t + a_n = dv / dt τ  +  v² / R ρ  ,

(1)

kde τ je jednotkový vektor v smere dotyčnice a ρ je jednotkový vektor smerujúci do stredu kružnice. Pre tangenciálne zrýchlenie a_t môžeme písať:

a_t = R ε

(2)

a pre normálové zrýchlenie a_n:

a_n = v² / R = ω² R  .

(3)

Pre veľkosť celkového zrýchlenia teda platí:

| a | = ( a_t² + a_n² )^1/2 = ( R² ε² + v⁴ / R² )^1/2  .

(4)

Uhlová rýchlosť ω a uhlové zrýchlenie εpohybujúceho sa bodu sú definované vzťahmi:

ω = dα / dt  ,

(5)

ε = dω / dt = d²α / dt²  ,

(6)

kde αpredstavuje vektor, ktorého hodnota je daná veľkosťou uhla opísaného polohovým vektorom pohybujúceho sa bodu. Súvis uhlovej rýchlosti ω s obvodovou rýchlosťou v pohybujúceho sa bodu po kružnici vyjadruje vzťah:

v = ω x R  _,

(7)

kde R je polomer kružnice. Keďže sa hmotný bod pohybuje po kružnici s konštantným uhlovým zrýchlením ε, pre uhlovú rýchlosť ωplatí:

ω = ∫ ε dt = ε t + ω₀  .

(8)

Keďže je uhlová rýchlosť na začiatku nulová (ω₀ = 0 rad.s^-1), pre uhlovú rýchlosť ω v ľubovoľnom čase t možeme písať:

  ω = ε t

 (9)

Po dosadení konkrétnych hodnôt dostávame pre uhlovú rýchlosť ω :

v = ω R

v = 8 s^-1 . 20 cm

v = 160 cm.s^-1

Získané hodnoty dosadíme do vzťahov (2), (3) a (4) pre výpočet veľkostí tangenciálneho a_t, normálového a_n a celkového zrýchlenia a:

a_t = 20 cm . 2 s^-2

a_t = 40 cm.s^-2

a_n = (160 cm.s^-1)² / 20 cm

a_n = 1280 cm.s^-2

a = [ (40 cm.s^-2)² + (1280 cm.s^-2)² ]^1/2

a = 1280,6 cm.s^-2

Hodnota celkového zrýchlenia v čase 4 s je 1280,6 cm.s^-2.

Absolútne čierne teleso