Hyperbolický vývoj vesmíru.

Vráťme sa teraz ku vzťahu, ktorý určuje polomer nášho vesmíru:

r = G . M / c² = 1,484 . 10 ²⁶ m

Ak náš vesmír vznikol prudkým rozopnutím superhustej hmoty sústredenej v nekonečne malom objeme, potom z daného vzťahu vyplýva, že rýchlosť svetla bola nekonečne veľká. My ju pri vzniku a vývoji vesmíru budeme postulovať. Nazveme ju hyperbolická a celú zodpovednosť za vznik, vývoj vesmíru a jeho charakteristické parametre ako sú polomer vesmíru, priemerná hustota vesmíru, teplota reliktného žiarenia atď. prenesieme na tento postulát, pričom z takto zavedenej rýchlosti sa stane koordinačný činiteľ vývoja vesmíru, ktorý tieto parametre určuje.

Rovnica, ktorá by mala pri rozpínaní vesmíru popisovať zmenu hyperbolickej rýchlosti až na súčasne meranú „konštantnú hodnotu“, musí vo svojej formule zahrňovať aj rotačný pohyb fyzikálneho systému. Prečo by to malo byť tak sa dozvieme v nasledujúcich úvahách, pri riešení problému Coriolisovej sily , problému kvarkov a antikvarkov a skutočnosti, že pomocou hyperbolických funkcií možno v najobecnejšej forme pre otočenie štvorrozmernej súradnicovej sústavy x, y, z, ct v rovine ct,x odvodiť Lorentzove relativistické súradnice priestoru a času pre prípad, že v čase t = 0 je x = 0. /1/

Takouto funkciou pri opise evolučného modelu vzniku a vývoja vesmíru bude hyperbolický kotangens:

y = coth x - kde hodnota argumentu tejto funkcie je udaná v radiánoch.

Opis zmeny hyperbolickej rýchlosti od času pre pozorovateľa umiestneného na Zemi rotujúcej okolo osi, alebo na inom rotujúcom kozmickom telese, ktorý si kladie otázku ako sa tu objavil náš vesmír môžeme vyjadriť rovnicou:

c_H= c_o.coth x = c_o.coth (K . t)

kde K je konštanta, do ktorej môžeme vhodným matematickým formalizmom zahrnúť dobu rotácie Zeme, alebo inej rotujúcej kozmickej sústavy okolo vlastnej osi. Tento formalizmus by sa mal stať opodstatnený vtedy, ak pozorovateľ umiestnený na inom rotujúcom kozmickom telese, s inou periódou rotácie okolo osi pri opise vývoja vesmíru príde k rovnakým výsledkom ako pozorovateľ na Zemi, o čom sa možno presvedčiť tak, že vlastnú dobu rotácie ľubovolného rotujúceho telesa vyjadríme ako násobok alebo diel vlastnej doby rotácie Zeme okolo osi. Takýto postup nám v danom modeli umožňuje aplikovať princíp kovariantnosti. Potom konštantu K môžeme vyjadriť:

K= 2p / T_o

a pre hyperbolickú rýchlosť c_H môžeme napísať nasledujúcu rovnicu:

c_H = c_o . coth (K . t) (5)

c_H - hyperbolická rýchlosť

T_o = 86164 s - doba rotácie Zeme okolo osi

K= 2p / T_o= 7,292.10 ^-5 rad. s ^-1

c_o - súčasne meraná rýchlosť svetla

t - náš pozemský gravitačný čas

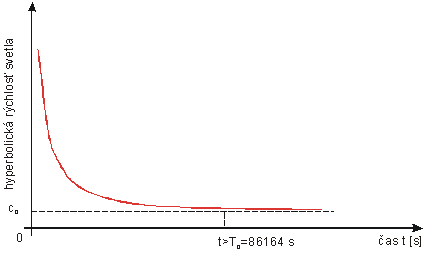
Grafickú závislosť hyperbolickej rýchlosti od času nám udáva obr. č.1

Obr.č.1

Ak v tomto modeli prijmeme predstavu svetelných hodín, tak vzhľadom na náš gravitačný čas odvodený od rotácie Zeme okolo osi, sa pri meniacej rýchlosti svetla môže definovať hyperbolický čas, ktorého grafická závislosť od nášho gravitačného času má rovnaký priebeh ako hyperbolická rýchlosť svetla (obr.č.1a) a určený je rovnicou (6)

t_H = T_o . coth (K . t) (6)

t_H - hyperbolický čas v expandujúcom vesmíru vyjadrená v „hyperbolických“ sekundách

T_o- _{perióda rotácie planéty okolo osi, vzhľadom na ktorú budeme opisovať časo-priestorový vývoj vesmíru}

_{pomocou gravitačného času, odvodeného z doby rotácie planéty}

t - gravitačný čas v sekundách

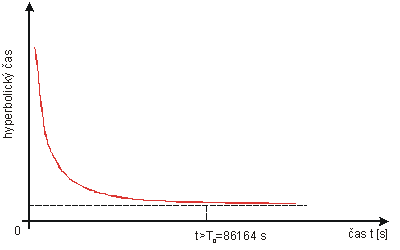
obr.č.1a

Môžeme sa opýtať, aký fyzikálny význam má zavedenie hyperbolického času? Zo všeobecnej  teórie relativity vyplýva, že keď svetelný signál opúšťa povrch hmotného objektu, dochádza k javu, ktorý nazývame gravitačný červený posuv. To znamená, že vlnová dĺžka vyžiareného svetelného signálu sa pri vzďaľovaní od hmotného objektu posúva k väčším vlnovým dĺžkam a súčasne platí, že hodiny na povrchu kozmického telesa sa opozďujú za hodinami, ktoré sú vo väčšej vzdialenosti od gravitačného stredu telesa (vo väčšej výške nad povrchom telesa) podľa vzťahu :

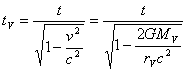(6a)

t_v–čas atómových hodín na povrchu kozmického telesa o polomere R

t –čas atómových hodín vo výške h nad povrchom, tj. vo vzdialenosti r_v = R + h

G- gravitačná konštanta

M_V - hmotnosť telesa

r_v –vzdialenosť od gravitačného stredu

c - rýchlosť svetla

K akému záveru dospejeme pri opise vzniku a vývoja vesmíru, ak porovnáme rovnice (6) s rovnicou (6a) ?

Pomer zmeny hyperbolického času za gravitačný čas: Dt_{H /} t určený z rovnice (6) nám udáva zrýchlenie chodu hodín pri expanzii vesmíru. Z grafickej závislosti (obr.č.1a) a výpočtom možno dokázať, že táto zmena je približne v čase t= 10⁵ s už rovná nule. To znamená, že približne od času t= 10⁵ s sa hyperbolický čas vo vesmíre stáva identický s gravitačným časom.

Rovnica (6a) potvrdzuje experiment s atómovými hodinami, ale úplne zlyháva pri opise vývoja vesmíru, pretože ak za r_{v = 0 - 1.4. 10}²⁶ m a M_v=2.10⁵³ kg dosadíme polomer a hmotnosť súčasne odhadovaného vesmíru, hodnota výrazu pod odmocninou od počiatku vývoja vesmíru až po súčasnosť je vždy záporná.

Z grafického priebehu rovnice (6) vyplýva, že hyperbolický čas exponenciálne klesá. To znamená, že náš vesmír sa správal ako expandujúca čierna diera, na povrchu ktorej by hypotetický pozorovateľ zistil, že čim je polomer vesmíru menší, tým je väčšie zakrivenie priestoru a času, ale už od času t = 10⁵ s  sa hyperbolický čas vo vesmíre stáva identický s gravitačným časom. Na základe toho, že pri opise vývoja vesmíru sa v časových dimenziách nemožno oprieť o rovnicu (6a) odvodenú zo všeobecnej teórie relativity, pretože v počiatočnej podmienke t = 0 je aj r = 0. Na základe tejto skutočnosti budeme opisovať vývoj vesmíru pomocou postulovanej hyperbolickej rýchlosti svetla.

Vráťme sa teraz k rovnici (4). Ak za c dosadíme hyperbolickú rýchlosť svetla :

c_H = c_o . coth (K . t )

pričom t predstavuje náš pozemský gravitačný čas potom pre závislosť polomeru vesmíru od času bude platiť nasledovná rovnica:

(7)

Hodnoty polomeru expandujúceho vesmíru (r₁) a hyperbolickej rýchlosti (c_H) v závislosti na čase udáva tabuľka č. 1.

Grafickú závislosť polomeru expandujúceho vesmíru od času je vyjadrená na obr.č.2

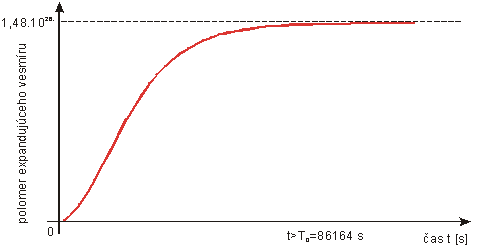
Obr.č.2

Závislosť hustoty látky od času.

V ďalšej časti nás bude zaujímať ako sa mení hustota látky vo vesmíre s časom; hmotnosť látky vo vesmíre v závislosti na objeme a hustote možno vyjadriť:

M = r.V = r.4/3.p.r³

dosadením za M do (7) bude pre hustotu platiť:

r = 3.c_H² / (4p.G.r² ) (8)

Zmenu hustoty r v závislosti na čase udáva tabuľka č.1. Musíme si ale uvedomiť, že táto závislosť nezohľadňuje vytváranie nových štruktúr pri vývoji vesmíru, ale určuje len jeho priemernú hustotu.

Závislosť teploty reliktného žiarenia od času.

Teraz nás bude zaujímať, ako sa mení teplota reliktového žiarenia v expandujúcom vesmíre? Keď predpokladáme, že v etape prudkého rozpínania vesmíru po vytvorení častíc prostredníctvom žiarenia sa počet fotónov nemení musí platiť Plancov zákon, podľa ktorého keď sa rozmery vesmíru zväčšili p-krát, vlnová dĺžka fotónov sa musí zväčšiť tiež p-krát: /1/ p = r / r₁ a p=l / l₁

r, l - polomer vesmíru a vlnová dĺžka po „relatívnom ukončení “ expanzie

r₁, l₁ - polomer vesmíru a vlnová dĺžka pri expanzii vesmíru

Pre „stacionárny“ vesmír sú r a  l v súčasnosti „konštantné“, pričom vlnovej dĺžke l a l₁ môžeme na základe Wienovho posuvného zákona priradiť teploty žiarenia podľa vzťahu:

l.T = b

T -termodynamická teplota

b - Wienova konštanta

l- vlnová dĺžka žiarenia

Z uvedených úvah za predpokladu, že teplota reliktného žiarenia v súčasnosti má hodnotu 2,7^oK možno napísať nasledovnú rovnicu: r / r₁ =l / l₁ = T₁ / T , po úprave pre závislosť teploty žiarenia v expandujúcom vesmíre bude platiť:

T₁ = T . r / r₁ = 2,7 . 1,458 . 10 ²⁶ / r₁ = 3,936 . 10²⁶ . c_H² / (G . M) (9)

T - teplota reliktného žiarenia po „relatívnom ukončení “ expanzie vesmíru (2,7⁰K)

r- polomer vesmíru po „relatívnom ukončení “ expanzie (1,458.10 ²⁶m)

r_{1 ,}T₁ - polomer a teplota pri expanzii vesmíru

Pozoruhodnou vlastnosťou rovnice (9) je, že spája kvantový jav s gravitáciou a hyperbolickou rýchlosťou svetla. Zmenu teploty reliktného žiarenia od času udáva tabuľka č. 1. Ak sledujeme hodnoty teploty reliktného žiarenia a polomeru expandujúceho vesmíru pričom budeme predpokladať , že súčasne dochádza i k tvorbe galaxií (rovnica 21/2 ) a hviezd, potom by hypotetický pozorovateľ, ktorého zrakový vnem spadá do oblasti viditeľného žiarenia mohol tento proces pozorovať až vtedy, keď teplota reliktného žiarenia klesne pod hodnoty odpovedajúce vlnovým dĺžkam viditeľného žiarenia. Do tejto chvíle sa mu bude vesmír javiť ako žeravá guľa. Z tabuľky č.1 môžeme odhadom zistiť, že proces expanzie takého vesmíru je možné pozorovať približne až od času t=360 s, kedy polomer vesmíru bol rádovo 10 ²³ m a teplota reliktného žiarenia približne 3700 ⁰K(vesmírne objekty sa postupne stávajú viditeľné t.j. nastáva čerenie vesmíru tak, ako keď zmizne hmla a objaví sa nádherná panoráma prírody ). Tento jav, ktorý sa uskutočnil v prvých sekundách vývoja vesmíru, by mal zanechať stopu v reliktnom žiarení, pretože základné štruktúry vesmíru (galaxie) v tomto čase-ako sa dozvieme v kapitole „Coriolisova sla“- už existovali. Na základe takéhoto opisu by sme mohli prehlásiť, že čím sú od nás galaxie vzdialenejšie, tým sa nám javí ich hustota väčšia, čo pozorovania vzdialených galaxií potvrdzujú. Z tabuľky sa dá zistiť, že pri poklese teploty reliktného žiarenia na 2,7 ^oK sa polomer vesmíru pri takomto opise zväčšil približne tisickrát. Z týchto úvah môžeme prísť k uzáveru, že to čo pozorujeme pri sledovaní vzdialených galaxií (posun spektrálnych čiar k červenému okraju spektra) je stopa javu, ktorý sa odohral v ranných štádiách vývoja vesmíru oveľa rýchlejšie než v súčasnosti predpokladáme, pričom pozorujeme obraz vzdialených galaxií až v čase, keď vesmír mal rozmery rádove 10²²až 10²³ m a žiarenie už bolo oddelené od látky. To ale znamená, že čím je súčasne pozorovaný objekt vzdialenejší, tým bol jemu odpovedajúci vesmír menší, pričom každá fyzikálna štruktúra (kopy galaxií a galaxie) je medzi sebou kauzálne prepojená svetelným signálom. Ztohoto dôvodu musíme rozlišovať v expandujúcom vesmíre udalosti, keď v súčasnosti sledované fotóny vzdialených galaxií nám podávajú informáciu o vesmíre, ktorého rozmery boli oveľa menšie. Môžeme teda konštatovať, že pri súčasnom pozorovaní a analýze žiarenia expandujúceho vesmíru ide o istý druh hysterézie, kedy sa následok oneskoruje za príčinou. Spomínanú argumentáciu potvrdzuje aj skutočnosť, že podľa Plancovho zákona žiarenia v rozpínajúcom vesmíre by mala teplota reliktného žiarenia klesať, ale my od čias ako sme ho objavili pred viac ako tridsiatimi rokmi zisťujeme, že jeho teplota je stále 2,7 ⁰ K. To by ale znamenalo, že rozpínanie vesmíru a tomu odpovedajúci pokles teploty reliktného žiarenia je tak pomalý, že súčasnými meracími metódami nemožno merať jeho pokles. Čo to ale znamená? Ak sú svetelné objekty vesmíru vzdialené od pozorovateľa v oveľa väčšej vzdialenosti akú prejde svetlo za jednu sekundu, potom súčasná analýza svetla pozorovateľom na Zemi nám podáva informáciu o časopriestorovej minulosti vesmíru. To znamená, že „moje teraz na Zemi“ nie je identické s „iným teraz pre pozorovateľa“, ktorý je od Zeme vzdialený niekoľko miliard svetelných rokov.

Čo to znamená pre komunikačný systém vo vesmíre na veľké vzdialenosti (svetelné roky až miliardy svetelných rokov) ? Odpoveď je jednoduchá. Takáto informačná komunikácia, ktorej obsahom je promptné riešenie problému nie je možná, pretože príjem informácie pozorovateľom na Zemi v tomto okamihu a jej replika je pre veľmi vzdialeného pozorovateľa bezpredmetná, nakoľko táto informácia dospeje k vzdialenému pozorovateľovi, ktorý je od nás vzdialený tisíc svetelných rokov s oneskorením (tisíc rokov). Ako príklad komunikácie na veľkú vzdialenosť môžeme uviesť nasledujúcu fabulu: „Vzdialenosť Moskva - Washington je tisíc svetelných rokov. Washington príjme dôležitú diplomatickú informáciu (teraz vo Washingtone) z Moskvy a musí sa o dve hodiny rozhodnúť a poslať repliku depeše do Moskvy. Moskva príjme informáciu repliky z Washingtonu až o dvetisíc rokov plus dve hodiny (teraz v Moskve)od okamihu vyslania depeše z Moskvy. V súčasnosti je náš letopočet rok 2002, viete čo bolo na Zemi pred dvetisíc rokmi? Viete – Washington neexistoval (ak budeme dôsledný ani Moskva). Sami uznáte, že takáto komunikácia na oveľa väčšie vzdialenosti, ktoré sa počas komunikácie nemenia sa stáva pri riešení promptných problémov nemožná. Situácia sa ešte viac skomplikuje, ak sa vzdialenosti oboch miest menia.