Corolisova sila pri vzniku a vývoji vesmíru v rotujúcom gravitačnom poli.

Našou úlohov bude opísať správanie sa „hmotných bodov“ v neinerciálnej sústave S spojenej s  rotujúcim gravitačným poľom, v ktorom sa pri expanzii vesmíru menil polomer a rýchlosť hmotných bodov. Teraz pri výpočte zmeny momentu hybnosti hmotných bodov v rotujúcom gravitačnom poli radiálnu a normálovú zložku rýchlosti hmotných bodov nemožno považovať za konštantnú. Ich rýchlosť v expandujúcom vesmíre vzhľadom na neinerciálnu sústavu S spojenú s rotujúcim gravitačným poľom  rozložíme na jej radiálnu zložku v_r a na zložku normálovú v_n kolmú na v_r . Rýchlosť hmotných bodov voči neinerciálnej sústave S môžeme vyjadriť vektorovou rovnicou: v_s= dr /dt = v_r + v_n = v_r + (w × r )

Sústavu S bude teda tvoriť rotujúce gravitačné pole, ktoré sa vytvorilo v okamihu interakcie žiarenia s poľom s nulovým spinom, tj s takou formou inobytia, ktorá existovala pred veľkým treskom a o ktorom nemá fyzika žiadnu informaciu. Až po tejto interakcii v kontexte s princípom kauzality, kvantovým princípom, princípom symetrie, korešpodencie,kovariantnosti a filozofickými princípmi nastupuje na scénu priestor a čas tj. bytie v našom vesmíre s prírodnými a filozofickými princípmi.

V kontexte s princípom kauzality a kvantovým princípom možno vznik a vývoj vesmíru racionálne opísať iba tak, že príčinou jeho vzniku bolo žiarenie s extrémne vysokou energiou, ktorého prítomnosť pri tomto neopakovateľnom fenoméne možno len postulovať. Toto žiarenie ako príčina, na ktorú prenesieme všetku zodpovednosť za vznik a vývoj vesmíru súvisí s následkom, ktorého ovocím pri interakcii s poľom s nulovým spinom sa stal náš bipolárny vesmír s protikladmi, ktoré nemožno odstrániť. Súčasne treba zdôrazniť, že výsledkom tejto interakcie bolo generovanie obrovského množstva látky s extrémne vysokou teplotou a hustotou, z ktorej pri expanzii vznikli pri jeho vývoji na základe fyzikálnych interakcií súčasne pozorované štruktúry vesmíru. Tento fenomén zmeny stavu, pri ktorom z inobytia vzniklo bytie tj. vesmír, sa musel uskutočniť konaním práce, v kontexte so základným fyzikálnym a filozofickým princípom, podľa ktorého každá zmena stavu je spojená s konaním práce. Podľa kvantového princípu, túto prácu pri vzniku a vývoji vesmíru vykonalo žiarenie a dá sa dokázať, že toto žiarenie sa stalo koordinačným činiteľom, ktorý vo vesmíre pri jeho vývoji určoval jeho charakteristické parametre, ako sú hustota, teplota reliktného žiarenia a štruktúra vesmíru s jeho geometriou. Možno dokázať, že náš vesmír je vhodne modulovaná nula. Príčinou modulácie tejto nuly s konkrétnymi vesmírnymi štruktúrami bolo žiarenie, ktoré ako svedok interakcie s poľom s nulovým spinom sa v našom vesmíre nachádza ako reliktné žiarenie s teplotou 2.7 ⁰K. Pokúsme sa racionálne sprístupniť fenomén rotujúceho gravitačného poľa, ktoré zohralo a zohráva v súvislosti s Coriolisovou silou rozhodujúcu úlohu pri vývoji a súčasnom stave vesmíru.

Predstavu rotujúceho gravitačného poľa možno pripodobniť k činnosti trojfázového asynchrónneho motora,

v ktorom rotujúce magnetické pole na princípe fyzikálnych zákonov dokáže roztočiť rotor alternátora, ktorého

frekvencia otáčok zaostáva za otáčkami magnetického poľa.

Na základe druhej vety impulzovej pre moment sily pôsobiacej na hmotné body v rotujúcom fyzikálnom systéme vzhľadom na neinerciálnu sústavu S bude platiť po dosadení za v_s= dr /dt = v_r + v_n = v_r + (w × r ) nasledujúca rovnica:

M = dL / dt = r × F = m. d[ r × v_s ] / dt = m.d[ r × ( v_r + ( w × r )] / dt = m.d[r × v_r + r × (w × r)] / dt =

M = dL / dt = r × F =m. [ dr / dt × (w × r) + r × ( dw / dt × r ) + r × (w × dr /dt ) ]

kde: r × v_r = 0

dw / dt = e a súčasne e < 0 - uhlové spomalenie rotujúceho systému pri expanzii vesmíru

Po dosadení za dr/dt do predchádzajúcej vektorovej rovnice a jej úprave môžeme pre pohybovú rovnicu rotujúceho fyzikálneho systému odvodiť výraz:

M = dL / dt = r × F = m.[v_r× (w × r) + (w × r) × (w × r) + r × (e × r ) + r × (w × v_r) + r × [w × (w × r)]

Pre zložený vektorový súčin platí: (w × r) × (w × r) = 0

Po týchto operáciách moment sily môžeme vyjadriť:

M = dL / dt = r × F = m[v_r × (w × r) + r × (e × r ) + r × (w × v_r) + r × [w × (w × r)] ] (X₀)

Rovnicu (X₀) možno pokojne nazvať pohybovou rovnicou evolučného modelu vesmíru. Prečo je to tak sa pokúsime dokázať v nasledujúcich tvrdeniach.

Moment sily expandujúceho vesmíru určený z predchádzajúcej rovnice sa bude skladať zo štyroch zložiek točivých momentov, pre ktoré platia rovnice:

M_r= m[v_r × (w × r) ] = r × F_r = r × m.a _r = r × m. dv_r /dt < 0 - točivý moment odvodený od radiálneho spomalenia expandujúceho vesmíru !!!

Me = m[r × (e × r ) ] - točivý moment odvodený od uhlového spomalenia expandujúceho vesmíru

M_cr= m[r × (w × v_r) ]- točivý moment odvodený od radiálnej zložky Coriolisovej sily v danom bode

M_cn= m[ r × [w × (w × r)] ] - točivý moment odvodený od normálovej zložky Coriolisovej sily v danom bode

Neinerciálnu sústavu S budeme zobrazovať vektorom uhlovej rýchlosti w rotujúceho gravitačného poľa vesmíru orientovaného zvisle nahor a rovinou kozmického rovníka (horizontálna rovina) preloženou počiatkom neinerciálnej sústavy S, na ktorú je kolmý vektor uhlovej rýchlosti w. Táto rovina myšlienkovo delí naš vesmír na severnú a južnú hemisféru. V kontexte s rovnicou (X₀) musíme zistiť, či sa hmotné body môžu pohybovať po ľubovolných trajektóriach. Z vyšie uvedevých štyroch točivých momentov vyplýva, že zakázané sú kruhové trajektórie pohybu hmoných bodov vzhľadom na rovinu roníka centrálneho telesa, pri ktorých je aspon v jednom bode trajektórie točivý moment odvodený od normálovej zložky Coriolisovej sily rovný nule. Tomutu točivému momentu odpovedá dostredivá sila F_cn = m[w ×(w × r )] , ktorá je na póle rovná nule, t.j. keď inklinácia trajektórie hmotného bodu k rovine rovníka centrálneho telesa je i=90⁰, potom točivý moment je v tomto bode nulový a odstredivá energia (rovnica č.26) E_od=1/2m.(w × r )²=1/2.m[ (wr )² - (w . r )²] =0 M_cn= m[ r × [w × (w × r)] ] = 0.

Druhá kruhová trajektória hmotného bodu, ktorej inklinácia k rovníku je i=0⁰ sa bude vyznačovať tým, že dostredivá sila F_cn = m[w ×(w × r )] nadobúda maximálnu hodnotu, ale točivý moment M_cn na tejto trajektórii je nulový: M_cn= m[ r × [w × (w × r)] ] = 0 tj. hmotný bod sa vzhľadom na pozorovateľa v rotujúcej neinercialnej sústave S otáča v danej vzdialenosti spolu s neinerciálnou sústavou tak, že sa mu pohybujúci hmotný bod javý tak, akoby sa nepohyboval vzhľadom na povrch centrálneho telesa, ktorého je satelitom a objeha v rovine kolmej na rotačnú os centrálneho telesa. Danú vzdialenosť možno určiť z ronosti gravitačnej a dostredivej sily, pričom odstredivá energia (rovnica č.27) E_od=1/2m.(w × r )²= 1/2m.(wr )² je maximálna.

Záver z analýzy pohybovej rovnice hmotného bodu (Xo) v rotujúcom gravitačnom poli je taký, že vo vesmíre nepozorujeme kruhové trajektórie hmotných bodov na orbitách, ktorých inklinácia k rovine rovníka rorujúceho gavitačného poľa centrálneho telesa je rovná i=0⁰ až i=180⁰, okrem prípadu, v ktorom je inklinácia i=0,⁰ odstredivá energia je maximálna, celková energia minimálna a trajektória je kruhová. Vzdialenoť hmotného bodu je taká, že dostredivá sila sa rovná gravitačnej sile. Ak sa hlbšie zamyslíme nad fyzikálnym významom štyroch točivých momentov môžeme zistiť dalšiu závažnú skutočnosť, ktorá má význam pre astronómiu a kozmonautiku: exaktne kruhová, alebo eliptická trajektória hmotného bodu pre inklináciu i=90⁰ nemôže v celom vesmíre existovať. To znamená, že na polárnu trajektóriu nemožno umiestniť žiaden satelit.

Vektory M_r a  M_cr majú rovnaké umiestnenie, ale opačnú orientáciu smeru. Pre dané vektory možno napísať ronice: M_r= m[v_r × (w × r) ] = r × F_r = r × m.a_r , pričom pri radiálnom spomalení expandujúceho vesmíru je radiálne zrýchlenie (viď obr.č. 4a) a_r = dv_r /dt < 0 !!!

a pre točivý moment odvodený od radiálnej zložky Coriolisovej sily platí: M_{c r}= m[r × (w × v_r) ]= r × F_{c r}

Rovnicu (X₀) môžeme potom napísať v tvare:

M = dL / dt = r × F = m[ r × ( F_r + F_{c r} + F_e + F_cn) ] (X₁)

A vektorový súčet síl pôsobiacich na hmotný objekt možno vyjadriť podľa (X₀) rovnicou (X₂) :

F = m.[ dv_r /dt + (w × v_r ) + ( e × r ) + w × (w × r ) ] (X₂)

Prvý výraz v zátvorke vyjadruje radiánu silu pri radiálnom spomalení expanzie, druhý a štvrtý výraz predstavuje radiálnu a normálovú zložku Coriolisovej sily, tretí výraz súvisí s uhlovým spomalením. Pre dané sily môžeme napísať vsťahy:

1.F_r = m. a_r = m.dv_r /dt 3.F_e = m. (e × r )

2.F_cr = m.(w × v_r ) 4.F_cn = m[w ×(w × r )]

Umiestnením vektora F_cr je normálová zložka rýchlosti v_n. Sila F_cn je kolmá na vektor w a pri pohybe hmotných bodov v rotujúcom gravitačnom poli bude predstavovať dostredivú silu pôsobiacu na hmotné body. Výraz: F_e = m.( e × r ) reprezentuje silu, ktorá súvisí so spomalením a_e = ( e × r ) rotácie fyzikálneho systému, má opačný smer ako vektor F_{c r}, alebo vektor (w × r ) a súhlasný ako vektor F_r.

Pokúsme sa teraz opísať pohyb častíc v expandujúcom vesmíre. Zvoľme si dve vzťažné sústavy S a S , ktoré majú spoločný začiatok. Prvá sústava bude inerciálna a druhá sa vzhľadom na ňu bude otáčať uhlovou rýchlosťou w . Sústava S bude teda neinerciálna./1/

Môžeme sa opýtať - čo sa tu bude otáčať? Pri racionálnom opise evolučného modelu vesmíru možno predpokladať, že to bude rotujúce gravitačné pole, pričom tento proces by mal mať pri vzniku vesmíru povahu kvantového javu, pri ktorom sa z pôvodnej prainterakcie oddelila ako prvá gravitačná interakcia. My budeme opisovať pohyb častíc z hľadiska neinerciálnej sústavy S.

Ak z pohľadu inerciálnej sústavy je rýchlosť častíc radiálna, potom rýchlosť častíc z hľadiska neinerciálnej sústavy S sa skladá z jej radiálnej rýchlosti vzhľadom na sústavu S (v_r ) a rýchlosti jej otáčania v_n= (w × r ) spolu so sústavou S , čo môžeme vyjadriť rovnicou:

v_(s)= v_r + ( w × r ) (12)

Polohový vektor hmotných bodov v obidvoch sústavách je totožný!

Skúmajme teraz, či možno takýto opis vývoja vesmíru aplikovať na náš model. Ak rovnicu (7) zderivujeme podľa času, dostaneme nasledujúcu rovnicu:

v_n = dr/dt = 2KGM.sinh(Kt) / [c_o².cosh³(K.t)] (13)

táto rovnica bude predstavovať veľkosť normálovej zložky rýchlosti častice v rotujúcom gravitačnom poli.

Rovnicu (13) môžeme formálne upraviť na tvar:

v_n= [GM tgh²(Kt) / c_o² ]. [4K / (2sinh(Kt) cosh(Kt)]

V takto upravenej rovnici prvý zlomok predstavuje polomer expandujúceho vesmíru a druhý zlomok veľkosť uhlovej rýchlosti rotácie objektu v rotujúcom gravitačnom poli. Rovnica (13) bude vyjadrovať normálovú zložku rýchlosti častíc v rotujúcom gravitačnom poli, a výraz:

(14)

určuje ich uhlovú rýchlosť rotácie. Keď zderivujeme rovnicu (14) podľa času, môžeme vyjadriť vzťah pre

uhlové spomalenie : (15)

Radiálnu zložku rýchlosti častíc v rotujúcom poli určuje rovnica, ktorú sme odvodili pre radiálnu rýchlosť častíc po interakcii žiarenia s poľom s nulovým spinom:

v_r = Ö3.c_H / 2 = Ö3. c_o / [ 2tgh(Kt) ] (16)

Výslednú rýchlosť vzhľadom na neinerciálnu sústavu môžeme vyjadriť ako vektorový súčet rýchlosti v_r a v_n:

v_s = v_r + v_n kde v_n= ( w × r )

Ak rovnicu (12) zderivujeme podľa času, odvodíme rovnicu, ktorá určuje veľkosť absolutného zrýchlenia

vzhľadom na neinerciálnu sústavu S :

(17)

V rovnici (17) vystupuje výraz dr/dt, ktorý určuje rýchlosť hmotného bodu vzhľadom na neinerciálnu sústavu S. Pretože rýchlosť hmotného bodu v expandujúcom vesmíre vzhľadom na neinercialnu sústavu S môžeme rozložiť na radiálnu zložku v_r , ktorá má smer polohového vektoru r a na zložku normálovú v_n= w × r, ktorá je kolmá na vektor v_r , bude výraz dr/dt v rovnici (17) predstavovať rýchlosť hmotného bodu vzhľadom na neinercialnu sústavu S, pre ktorú bude platiť:

dr/dt = v_s = v_r + (w × r )

Po úprave výraz w ´ dr/dt možno vyjadriť : w ´ dr/dt = w ´ [v_r + (w × r )] = (w × v_r ) + w × (w × r )

Výraz : a_cr= (w × v_r ) ; určuje radiálnu zložku Coriolisovho zrýchlenia, ktorej umiestnením je normálová zložka rýchlosti v_n a a_cn = a_d = w × (w × r ) = w (w . r ) – r (w. w ) - určuje normálovú zložku Corolisovho zrýchlenia, ktorého umiestnením je vektor kolmý na vektor w .Daný výraz reprezentuje dostredivé zrýchlenie hmotných bodov v rotujúcom gravitačnom poli. Výrazy v zátvorkách vyjadrujú skalárne súčiny vektorov .

Veľkosť vektoru a_cn= a_d môžeme vypočítať tak, že polohový vektor r vyjadríme ako vektorový súčet vektorov r_o a a_o, pričom r_o má smer uhlovej rýchlosti w a a_o je kolmý na w , čo môžeme podľa obr. č. 3 zapísať rovnicou : r = r_o + a_o

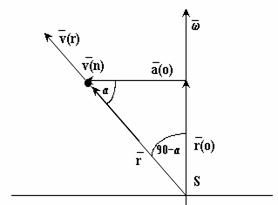
Obr. č.3

v_n- je vektor kolmý na rovinu r a w pričom je orientovaný k nám. Pre veľkosť normálovej zložky Coriolisovho zrýchlenia, ktorá určuje dostredivé zrýchlenie: a_cn= a_d môžeme odvodiť výraz:

a_d = w × [w × ( r_o+ a_o )] = w × (w × r_o) + w × ( w× a_o ) = w × (w × a_o)

kde: (w × r_o) = 0

Pre zložený vektorový súčin platí :

a_d = w × (w × a_o ) = w (w . a_o ) – a_o ( w. w ) = – a_o ( w . w ) Po vynásobení poslednej rovnice jednotkovým vektorom v smere a_o pre veľkosť a_d dostaneme rovnicu : a_d = - a_o. w ² = - r. w ². cos a ; pričom w . a_o =0 a a je uhol, ktorý zviera vektor r s vektorom a_o .

Po dosadení za w ´ dr/dt do (17) získame nasledujúcu rovnicu pre absolútne zrýchlenie a_(s) vzhľadom na neinerciálnu sústavu S :

a_(s)= dv_r /dt + e ´ r + w ´ v_r + w ´ (w ´ r) (18)

Jednotlivé výrazy v (18) reprezentujú:

dv_r /dt =a _r -radiálne zrýchlenie hmotných bodov v gravitačnom poli, pričom vekosť a _r < 0

e ´ r = a _(e) -zrýchlenie súvisiace so spomalením rotácie pri expanzii vesmíru

w ´ v_r = a _{c r} -radiálna zložka Coriolisovho zrýchlenia

w ´ (w ´ r) = a_{c n} - normálová zložka Coriolisovho zrýchlenia predstavuje dostredivé zrýchlenie( a_cn = a_d )

Celkové zrýchlenie hmotných bodov v rotujúcom a expandujúcom gravitačnom poli vzhľadom na neinerciálnu sústavu S môže vyjadriť ako vektorový súčet týchto zrýchlení:

a_(S) = a_r + a_e + a_cr+ a_cn (19)

V rovnici (19) vystupuje radiálne zrýchlenie, ktoré odvodíme z rovnice (16) jej derivovaním podľa času:

(20)

Dostredivá sila je kolmá na vektor uhlovej rýchlosti w rotujúceho gravitačného poľa. Radiálna sila F_r, ktorá udáva radiálne spomalenie pri expanzii vesmíru sa vyznačuje tým, že v rotujúcom gravitačnom poli je jej umiestnením polohový vektor F_e . Názornejšie je daná situácia zobrazená na vektorovom diagrame obr. č .4 !!!

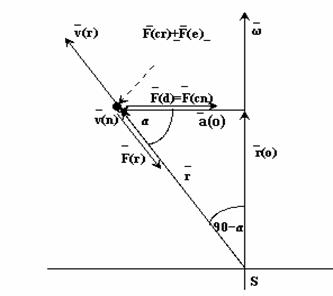
Obr.č.4

v_{(r )} - radiálna zložka rýchlosti

v_(n) - normálová zložka rýchlosti, kolmá na rovinu r a w pričom smeruje k nám

F_(d) = F_cn - vektor dostredivej sily, ktorý predstavuje normálovú zložku Coriolisovej sily F_cn odvodenej od normálovej zložky rýchlosti (v_n )

F_(cr) - rádiálna zložka vektora Coriolisovej sily odvodená od radiálnej zložky rýchlosti v_r v danom bode , ktorá má smer vektora v_n

F(e) = F(e) -vektor sily, ktorý súvisí s uhlovým spomalením e fyzikálneho systému a ktorý je

v expandujúcom vesmíre opačne orientovaný ako vektor F_{(c r)}

F_r - vektor radiálnej sily pri radiálnom spomalení expanzie vesmíru. Jeho umiestnením v radiálnom

gravitačnom poli by bol vektor orientovaný do gravitačného stredu ale v expandujúcom a  rotujúcom gravitačnom poli je jeho umiestnením vektor F(e) (viď obr. č. 4a )

Hodnoty radiálnej rýchlosti, uhlovej rýchlosti , podielu radiálnej rýchlosti a uhlovej rýchlosti, radiálneho zrýchlenia, radiálnej a normálovej zložky Coriolisovho zrýchlenia, zrýchlenia súvisiaceho s uhlovým spomalením rotácie e pri expanzii vesmíru a rozdielu (a_cr – a_e – a_r) sú uvedené v tabuľke číslo 2 . Nasledujúci opis javov bude vychádzať z vektorového diagramu (č. 4 ) a (č. 4a).

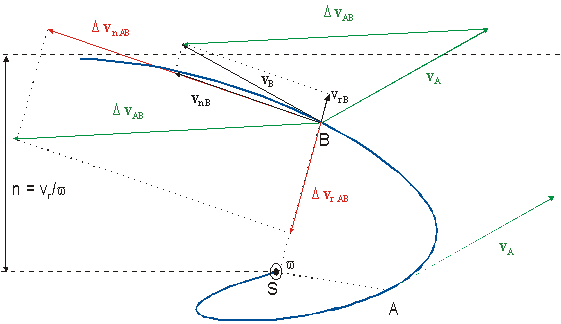
Obr. č. 4a

Dv_AB, Dv_{r AB}, Dv_{n AB} – zmena rýchlosti, zmena radiálnej a normálovej zložky rýchlosti Dv_AB na trajektórii AB

v_{n B}, v_{r B} - normálová a radiálna zložka rýchlosti v _B v bode B

n = v_r / w = konštanta (viď v nasledujúcich riadkoch) - vzdialenosť asymptoty trajektórie (hyperbolickej špirály) hmotného objektu od gravitačného sredu

w - vektor uhlovej rýchlosti rotujúceho objektu v rotujúcom gravitačnom poli vesmíru, ktorý je kolmý na rovinu preloženú počiatkom neinercialnej sústavy S a na obr. č. 4a smeruje k nám, pričom inklinácia trajektórie hmotného bodu je väčšia ako nula. Táto rovina rozdeľuje naš vesmír na dve hemisféry (severnú a južnú).

O normálovej zložke Coriolisovej sily F_{(c n)} už vieme, že je silou dostredivou a kolmou na vektor uhlovéj rýchlosti w .Vektor sily F(e) , ktorý súvisí s uhlovým spomalením rotujúceho fyzikálneho systému leží na vektorovej priamke vektora F_{(c r)} , ale má opačnú orientáciu smeru. Vektor radiálnej sily F_r, ktorý súvisí s radiálnym spomalením bude mať v rotujúcom gravitačnom poli opačný smer ako vektor F_{(c r)} ( viď obr. č. 4a ), alebo pri uhlovom spomalení expandujúceho vesmíru je jeho umiestnením vektor F(e) .

Skúsme sa teraz zaoberať otázkou, ako zistiť čas, v ktorom došlo k rozpadu expandujúceho vesmíru na kopy galaxií a galaxie.

V danom systéme by mala nastať zmena kvality fyzikálneho systému až po dosiahnutí určitej kvantitatívnej zmeny fyzikálnych veličín. Takúto kvalitatívnu zmenu by mohol vyvolať stav, kedy sa vektorový súčet radiálnej zložky Coriolisovej sily F_{(c r)} , sily F(e) a sily F_r v expandujúcom vesmíre rovná nule. Tieto tri sily ležia na jednej priamke, pričom posledné dve majú pri expanzii opačnú orientáciu smeru ako sila F_{(c r)} .To znamená, že bude platiť rovnica:

.V čase, v ktorom je výslednica týchto síl rovná nule bude na hmotný objekt(častice) pôsobiť iba dostredivá sila, ktorú reprezentuje normálová zložka Coriolisvej sily F_(cn) kolmá na rotačnú os daného fyzikálneho systému. Výslednica všetkých síl v danom okamihu by mala zmeniť stav fyzikálneho systému skokom pri splnení vyššie uvedenej rovnice tak, že súčasne by mala nastať fragmentácia vesmíru na kopy galaxií, pri ktorej by z pôvodného vesmíru pretiekla celá jeho hmota do rotujúcich kôp galaxií. Podľa rovnice (X₁) sa pri vytváraní nových kvalít z troch točivých momentov v danom okamihu uplatnil iba točivý moment odvodený od dostredivej sily F_cn. Možno predpokladať, že podobný proces by prebiehal i pri rozpade galaxií na hviezdokopy a hviezdy. Pri takomto opise vývoja vesmíru si môžeme položiť otázku, ako sa pohybovali fyzikálne objekty v rotujúcom gravitačnom poli do okamihu, kedy sa normálová zložka rýchlosti rotujúceho objektu číselne vyrovná jeho radiálnej zložke, pričom sa výpočtom možno presvedčiť, že práve vtedy je vektorový súčet vektorov F_{(c r)} , F(e) a F_r rovný nule.

Splnenie tejto podmienky vyžaduje postulát, podľa ktorého sa žiaden fyzikálny objekt nemôže pohybovať väčšou rýchlosťou ako je rýchlosť svetla. Hodnoty normálovej zložky rýchlosti v_n ,ktoré sú uvedené v tabuľke č.1 od okamihu rozpadu vesmíru na galaxie(kedy sa vektorový súčet vektorov F_{(c r)} , F(e) a F_r rovná nule) nebudú mať už v ďalšom vývoji vesmíru fyzikálny význam, ale hodnoty radiálnej rýchlosti v_r musíme pri nasledujúcom vývoji vesmíru rešpektovať. V kapitole „Radiálna rýchlosť fyzikálnych objektov v expandujúcom vesmíre“ sme uviedli, že podľa Heisembergovho princípu neurčitosti je rýchlosť častíc v jadre atómu rádovo rovná10⁸ m.s¹.Podľa výpočtov uvedených v tabuľke č.1 je radiálna rýchlosť častíc po „ukončení“expanzie(pretože sa jej veľkosť nemení) v_r= 2,5. 10⁸ ms^-1.

K akým uzáverom by sme mohli dospieť na základe týchto hodnôt radiálnej rýchlosti? Jedno z možných vysvetlení by mohla byť skutočnosť, že pri fragmentácii vesmíru na galaxie, by sa radiálna rýchlosť častíc pretransformovala pri vzniku nových štruktúr (vznik nukleónov a jadier prvkov) v dôsledku silnej interakcie do rýchlosti častíc jadra. Takáto predstava by mohla byť opodstatnená iba vtedy, ak by fyzikálne podmienky pre takýto proces korešpondovali s daným javom. Fyzikálnymi veličinami, ktorými by sme danú stavovú zmenu opísali, by mali byť teplota žiarenia a hustota látky. V nasledujúcich riadkoch sa dozvieme, že hustota látky a teplota žiarenia v danom stave vesmíru dosiahla tieto.hodnoty (tab.č.1): r = 8,46.10 ¹⁵kg m^-3, T= 2,24.10 ^{14 o}K. Výpočtami z kvantovej a relativistickej fyziky sa môžeme presvedčiť, že daná teplota je vyššia ako teplota tvorby neutrónov a jadier najstabilnejších prvkov. Na ilustráciu môžeme uviesť teploty tvorby uvedených štruktúr hmoty- neutrónov a jadier železa : T_(n)= 1,1.10 ^{13 o}K , T_(Fe)= 1,1.10 ^{11 o}K

Z daných výpočtov možno prísť k záveru, že pri fragmentácii vesmíru na nové kvality a štruktúry, látkovú formu hmoty by mohli tvoriť kvarky a antikvarky. Týmto problémom sa budeme zaoberať v kapitole „Problém kvarkov a antikvarkov“a v tematike „Tvorba jadier prvkov“.

V prípade, že trajektória fyzikálneho objektu je hyperbolická špirála (obr. č.4a), rýchlosť týchto objektov je daná dotyčnicou k trajektórii a pričom ju vždy môžeme vzhľadom na počiatok neinerciálnej sústavy rozložiť na radiálnu a normálovú zložku. Prečo tu bez dôvodu uvádzame, že trajektória hmotných bodov je hyperbolická špirála? Ak v tomto modeli vesmíru zistíme podiel veľkosti radiálnej rýchlosti sústavy a uhlovej rýchlosti v rotujúcom gravitačnom poli zistíme, že tento pomer je konštantný. Túto skutočnosť potvrdzujú výpočty v tabuľke č. 2. Hyperbolickú špirálu opisuje fyzikálny systém pohybujúca sa po lúči radiálnou rýchlosťou v_r, ktorý sa otáča okolo pólu (počiatok neinerciálnej sústavy) uhlovou rýchlosťou w. .Pretože fotóny reliktného žiarenia majú hmotnú povahu, po hyperbolickéj špirále sa budú pohybovať aj tjeto častice a hypotetický pozorovateľ by pozoroval tým menšie zakrivenie expandujúceho priestou, čím sú jeho rozmery väčšie. Rovina preložená kolmo cez počiatok neinerciálnej sústavy S a kolmá na rotačnú os vesmíru delí náš vesmír na dve hemisféry- severnú a južnú. Hmotné objekty smerujúce pri expanzii do oboch hemisfér budú vzhľadom na pozorovateľa v počiatku neinerciálnej sústavy S rotovať proti pohybu hodinových ručiciek. Ak si základnú „rovníkovú“ rovinu oboch hemisfér predstavíme ako zrkadlovú rovinu symetrie, potom by mali galaxie v oboch hemisférach vzhľadom na pozorovateľov -v symetrických galaxiách  vzhľadom na túto rovinu- rotovať v kontexte s princípom symetrie opačne – ako predmet a obraz v zrkadle.

Pre sprievodič hmotného bodu v polárnych súradniciach môžeme napísať rovnicu: r = n / φ

kde n = v_r/w je konštanta určená podielom radiálnej rýchlosti hmotného objektu a uhlovej rýchlosti rotujúceho objektu v rotujúcom gravitačnom poli a j - je uhlová dráha.

Teraz nás bude zaujímať otázka, kedy mohlo dôjsť k fragmentácii vesmíru na galaxie? Z diagramu síl č. 4 pôsobiacich v rotujúcom gravitačnom poli vyplýva, že by to malo nastať vtedy, keď pre vektorový súčet vektorov F_{(c r)} , F(e) a F_r bude platiť rovnica:

Grafickú závislosť veľkosti F_{(c r)} , F_r a F(e) od času udáva obr.č.5 .

Pomocou týchto síl možno ich zrýchlenia vyjadriť rovnicou: a_{c r}+ a_e + a _r = 0 a pre ich veľkosť v okamihu rozpadu (t= 0.0015 s) na galaxie bude platiť (viď tab. č 2 a obr.č.5):

a_{c r} = a_e + a _r = 2a_e (21/1).

Výpočtami uvedenými v tabuľke č.2 sa možno presvedčiť, že vznik novej kvality pre daný okamih nastane vtedy, keď veľkosť zrýchlenia a_{c r} sa číselne vyrovná veľkosti zrýchlenia a_e + a _r t.j. a_{c r} = a_e + a _r = 2a_e (viď obr.č.5)a ich vektorový súčet bude rovný nule. Potom bude platiť rovnica: 2a_e= a_{c r}

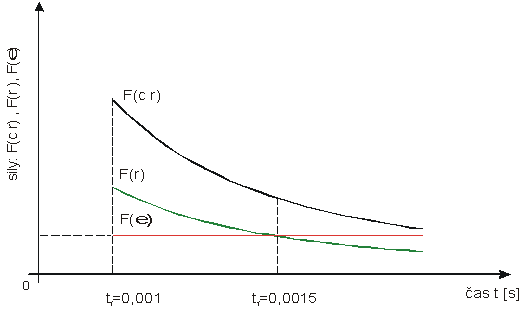
Obr.č.5

t = 0,0015s - predpokladaný čas fragmentácie vesmíru na galaxie

Po vyjadrení zrýchlenia a_e uhlovým spomalením e a polomerom r získame nasledujúcu rovnicu: 2e . r = a_{c r}

Ak do poslednej rovnice dosadíme za r, e ,w a v_r výrazy z rovníc 7, 14, 15 a 16 a upravíme tak, že vyjadríme

hmotnosť vesmíru, môžeme sa dopracovaťk nasledujúcej rovnici:

(21/2)

Za predpokladu, že hmotnosť vesmíru M_v=2.10⁵³kg, možno zistiť čas, v ktorom sa mohla odohrať fragmentácia vesmíru na galaxie: t = 0,0015 s. Tento predpoklad je opodstatnený, pretože podľa výpočtov uvedených v tabuľke č.1 sa hmotnosť vesmíru s časom nemení. Pozoruhodným javom, o ktorom sa možno presvedčiť výpočtom je, že čím je väčšia hmotnosť vesmíru, tým je jeho vývoj rýchlejší, čo je v súlade s kozmologickým princípom o vývoji hviezd. V rovnici (21/2) vystupuje podiel dvoch fundamentálnych konštánt: rýchlosti svetla a gravitačnej konštanty: c_o³/G = 4.10 ³⁵ kg.s ^-1.Táto veličina, ktorá má rozmer hmotnostného prietokového množstva látky a jej číselná hodnota, by mohla predstavovať hmotnosť objektov vzniknutých rozpadom vesmíru na galaxie(hviezdokopy),alebo inú kritickú hmotnosť objektov vznikajúcich pri fragmentácii vesmíru v čase, kedy k téjto udalosti došlo.

Pretože opis vývoja vesmíru na základe princípu kovariantnosti podľa modelu s hyperbolickou rýchlosťou je rovnaký pre každého pozorovateľa, môžeme v rovnici (21/2) ku spomínaným dvom konštantám zahrnúť aj konštantu K= 2p / T_o= 7,292.10 ^-5 rad. s ^–1. Ak vyjadríme číselnú hodnotu podielu c_o³/G.K=2,92 .10 ⁴¹ kg, potom uvedená hodnota by mala určovať hmotnosť galaxií. Ak sa oprieme o všeobecne platný údaj, že hmotnosť vesmíru je približne M_v=2.10⁵³kg, potom z rovníc ( 7 ),( 8 ) a ( 9 ) možno vypočítať polomer, priemernú hustotu vesmíru a teplotu reliktného žiarenia. Číselné hodnoty daných veličín v stanovenom čase fragmentácie nadobudli tieto hodnoty: r = 1,78.10¹² m, r = 8,46.10¹⁵ kg.m ^–3 a T = 2,24.10^{14 o}K.Vhodným matematickým formalizmom sme síce „určili“ hmotnosť galaxií, ale tento formalizmus nevysvetluje Hubbleom experimentálne zistený fakt, ktorý pravdepodobne pomýlil Einsteina, že väčšna galaxií sa od nás vzďaluje, ale sú aj také, ktoré sa k nám približujú. Ako vysvetliť túto skutočnosť? Ak uvážime, že pri fragmentácii vesmíru hmotnosť vznikajúcich vesmírnych štruktúr nebola rovná hmotnosti galaxií, ale hmotnosti kôp galaxií, potom existuje na Hubbleom experimentálne zistený fakt logické vysvetlenie. Predstavme si dva hmotné body(dve kopy galaxií), ktoré sa pri expanzii od seba vzďalujú. Ak sa vesmír rospínal tak, ako opisujeme, potom hmotný objekt s hmotnosťou druhej kopy galaxií by sa pri súčasnom rozpínaní vesmíru rozpadol vzhľadom na hypotetického pozorovateľa v prvéj kope galaxií tak, že niektoré galaxie z druhej kopy by sa od pozorovateľa vzďaľovali a tie, ktoré pri explózii telesa s hmotnosťou druhej kopy galaxií smerujú k pozorovateľovi by sa približovali. Pri analýze žiarenia, ktoré nám túto informáciu s oneskorením prináša, treba brať do úvahy súčasne Dopplerov aj  gravitačný posun vlnových dĺžok analyzovaného žiarenia.

Ako názorný príklad môže poslúžiť ohňostroj, pri ktorom dve svetlice, ktoré sa radiálne pohybujú rôznymi smermi explodujú. Ak si predstavíte, že sa nachádzate v jednej zo svetlíc, ktoré súčasne explodujú, budete sledovať explóziu druhej svetlice tak, že niektoré fragmenty sa budú k vám približovať a iné vzďalovať.

Nasledujúce úvahy budú vychádzať z poznatkov teoretickej fyziky (L.D.Landau - J.M.Lifšic: Úvod do teoretickej fyziky 1,ALFA 1980).

Budeme zaoberať energiou pohybujúcich sa materiálnych objektov v rotujúcom gravitačnom poli. Z teoretickej fyziky vieme, že Lagrangeova funkcia pre pohybujúci sa materiálny objekt má v neinerciálnej sústave S nasledujúci tvar:

(22)

L- Lagrangeova funkcia, v ktorej vystupuje kinetická a polohová energia materiálneho objektu, pričom je skalárnou funkciou.

Ak do rovnice (22) za rýchlosť v_s vzhľadom na neinerciálnu sústavu dosadíme výraz

z rovnice (12), získame Lagrangeovu funkciu v neinerciálnej sústave S:

(23)

Aby sme mohli vypočítať derivácie, ktoré vystupujú v Lagrangeovej rovnici(24):

(24)

kde výrazy: ; určujú hybnosť a silu pôsobiacu na daný materiálny objekt, musíme z rovnice (23) vypočítať hybnosť a túto dosadiť do vzťahu, ktorý určuje energiu materiálneho objektu v rotujúcom gravitačnom poli:

(25)

Výraz možno vyjadriť:

Po úprave a dosadení do rovnice (25) získame vzťah pre energiu materiálneho objektu:

(26)

Prvý výraz v rovnici (26) predstavuje kinetickú energiu, druhý predstavuje doplnkovú potenciálnu enargiu, ktorá sa nazýva odstredivá energia a tretí polohovú energiu. Výhodou nášho modelu je, že radiálnu rýchlosť materiálnych objektov, polohový vektor a uhlovú rýchlosť rotácie hmotného bodu možno určiť výpočtom a tak zistiť celkovú energiu fyzikálnych objektov pripadajúcu na jednotku hmotnosti. Číselnú hodnotu výrazu (w´r)² môžeme určiť z rovnice (13), pričom platí: (w´r)² =(wr)² - (w. r)² . Ak je uhol, ktorý zviera vektor w a vektor r rovný p/2, hodnota výrazu pre odstredivú energiu je maximálna a možno ju vyjadriť výrazom:

E_od=1/2m.(w × r )²= 1/2m.(wr )², ak je tento uhol rovný 0^o alebo p , potom je odstredivá energia rovná nule: E_od=1/2m.(w × r )²=1/2.m[ (wr )² - (w . r )²] =0

Predelením rovnice (26) hmotnosťou odvodíme rovnicu, ktorá vyjadruje celkovú energiu fyzikálnych sústav pripadajúcu na jednotku hmotnosti.

(27)

kde : M_o- hmotnosť vesmíru

m - hmotnosť telesa (hyperčastice)

Možno sa presvedčiť, že táto hodnota energie pripadajúca na jednotku hmotnosti v čase t = 10 ^–3 s je rádovo rovná: E / m = - 1,1.10 ³¹ J.kg ^-1

S podobným opisom javov sa môžeme stretnúť i pri pohybe planét okolo Slnka. Ich pohyb budeme opisovať z hľadiska neinerciálnej sústavy spojenej s rotujúcim gravitačným poľom umiestneným v strede Slnka. V tejto neinerciálnej sústave sa rýchlosť planéty skladá z jej radiálnej rýchlosti vzhľadom na sústavu S a z rýchlosti v_n= w ´ r jej otáčania spolu so sústavou S, čo môžeme vyjadriť rovnicou: v_s= v_r + (w ´ r )

Pre moment hybnosti planéty vzhľadom na rotujúcu sústavu S bude platiť:

Ak podľa diagramu č.4 vyjadríme polohový vektor planéty ako vektorový súčet r_o a a_o, kde r_o má smer vektora uhlovej rýchlosti rotácie gravitačného poľa a a_o je kolmý na r_o , môžeme pre moment hybnosti planéty napísať rovnicu:

(28)

Po úprave rovnice (28) a jej skalárnym vynásobením jednotkovým vektorom v smere vektora w môžeme pre veľkosť momentu hybnosti L odvodiť výraz:

L=m .w . a_o² (29)

kde w -je veľkosť uhlovej rýchlosti rotácie planéty v rotujúcom gravitačnom poli; a_o- je kolmá vzdialenosť planéty od vektora uhlovej rýchlosti gravitačného poľa Slnka

Parameter a_o - môžeme vypočítať pomocou polohového vektora planéty r a cosa :

a_o= r.cosa

kde a - je uhol, ktorý zviera vektor uhlovej rýchlosti rotácie centrálneho telesa okolo svojej osi v rotujúcom gravitačnom poli Slnka( w ) s vektorom dráhovej uhlovej rýchlosti ( W_E) planéty pri jej obehu okolo Slnka po ekliptike. Uhol a je teda uhol ,ktorý zviera rovina rotujúceho gravitačného poľa Slnka preložená slnečným rovníkom kolmo na vektor jeho uhlovej rýchlosti w s rovinou ekliptiky.Názornejšie si celú situáciu predstavíme podľa nasledujúceho diagramu:

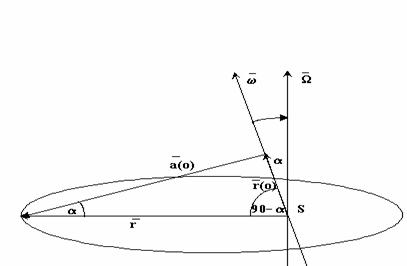
obr.č.6

Pri pohybe planét okolo Slnka bude na planétu pôsobiť ten istý typ síl, ktoré opisovali vývoj vesmíru pri jeho expanzii. Sú to: radiálna a normálová zložka Coriolisovej sily, zložka sily súvisiaca s radiálnym spomalením alebo zrýchlením planéty, zložka sily súvisiaca s uhlovým spomalením alebo zrýchlením planéty. Týmto silám možno priradiť ich zrýchlenia, ktorých umiestnenia sú analogické ako sme opisovali pri vývoji vesmíru, ale ich orientácia smeru je závislá od uhla (g) , ktorý zviera polohový vektor planéty s vektorom jej rýchlosti, ktorá je daná dotyčnicou k trajektórii v danom bode. Tento vektor je možné rozložiť okrem bodov obratu planéty ( perihélium a afélium ) na jeho radiálnu zložku v_r a normálovú zložku v_n Povedali sme, že smery vektorov spomínaných zrýchlení závisia od uhlu g. Ak je tento uhol tupý-pohyb od perihélia k aféliu,vektor a_cr má orientáciu smeru vektora v_n a vektor a_e a a_r je nesúhlasne orientovaný vzhľadom na smer vektora a_cr, pretože sa uhlová rýchlosť planéty zmenšuje .To znamená, že vektor uhlového spomalenia e má opačný smer ako vektor uhlovej rýchlosti w .V prípade, že uhol g je ostrý-pohyb od afélia k perihéliu, vektory a_cr a a_r + a_e zmenia orientáciu smeru na opačnú, než bola pri pohybe od perihélia k aféliu, pretože radiálna zložka rýchlosti v_r v tomto prípade smeruje k Slnku a vektor e má súhlasnú orientáciu smeru ako vektor w. Veľkosti týchto zrýchlení by sme mohli určiť z parametrov dráhy planéty zavedením polárnych súradníc a použitím zákona zachovania energie. Pokúsme sa teraz určiť na základe údajov v L.D.Landau-J.M.Lifšic: Úvod do teoretickej fyziky 1, ALFA 1980, pre danú planétu radiálnu rýchlosť v_r, uhlovú rýchlosť w pri jej obehu okolo centrálneho telesa a uhlové spomalenie e pri pohybe od perihélia k aféliu a uhlové zrýchlenie od afélia k perihéliu. Ak sa nám to podarí, potom pohybová rovnica planéty obiehajúca okolo centrálneho telesa bude mať presne ten istý tvar ako vyššie uvedená rovnica (X₀) :

M = dL / dt = r × F = m[v_r × (w × r) + r × (e × r ) + r × (w × v_r) + r × [w ×(w × r)] (X₀)

Ak budeme pri opise pohybu planéty okolo centrálneho telesa považovať planétu za hmotný bod, potom celá dráha pohybu hmotného bodu v centrálnom poli bude ležať v jednej rovine. Moment hybnosti hmotného bodu bude určovať nasledujúca rovnica:

L= m.r².dj /dt (X₃)

L- moment hybnosti planéty

m- hmotnosť planéty

r- vzdialenosť planéty od centrálneho telesa

dj /dt- uhlová rýchlosť otáčania planéty okolo centrálneho telesa

Úplný opis pohybu planéty v centrálnom poli najjednoduchšie vyjadríme, ak budeme vychádzať zo zákona zachovania energie.

Ak dj /dt vyjadríme pomocou (X₃) ako funkciu momentu hybnosti L ; (dj /dt= L/m.r²) dosadíme do výrazu pre celkovú mechanickú energiu E dostaneme rovnicu :

E= m. v²_s/2 + U_r = m.( v_r² + v²_n) /2 + U_r

E = m[(dr/dt)² + (r. dj /dt)²] /2 + U_r

v_s-rýchlosť planéty vzhľadom na neinerciálnu sústavu spojenú s rotačným gravitačným poľom centrálneho telesa, pre veľkosť ktorej platí: v_s²= v_r² + v_n²

v _r - radiálna zložka rýchlosti planéty

v_n= r. dj /dt - normálová zložka rýchlosti planéty

E= m. (dr/dt)²/2 + L²/2.m.r² + U_r (X₄)

Výraz: L²/2.m.r² – predstavuje odstredivú energiu

Z rovnice (X₄) pre radiálnu zložku rýchlosti v_r= dr/dt úpravou dostaneme rovnicu:

v_r= dr/dt = [ 2.( E – U_r)/m - L²/m².r² ]^1/2 (X₅)

Pre dt z rovnice (X₄) bude platiť:

dt = dr/ [ 2.( E – U_r)/m - L²/m².r² ]^1/2 (X₆)

Z rovnice (X₃) možno vyjadriť dj výrazom: dj = L/mr² .dt

Po dosadení za dt z rovnice (X₆) pre dj = L/mr² .dt bude platiť rovnica:

dj = L/mr² .dt = L / r².[ 2m( E – U_r) – L²/r² ]^1/2 .dr (X₇)

Uhlové spomalenie planéty možno zistiť pomocou rovnice (X₃) a dosadením za w= dj / dt do definičného vsťahu pre uhlové zrýchlenie:

e = dw/ dt = d(L/m.r²) /dt (X₈)

Za predpokladu, že sa moment hybnosti planéty mení ( výpočty momentu hybnosti planéty v perihéliu a aféliu planéty na konci tejto kapitoly), oblasť zmeny vzdialenosti planéty od centrálneho telesa má dve hranice: r_p - perihéliová a r_a - aféliová hranica.

Za čas, počas ktorého sa vzdialenosť planéty mení od perihélia (r_p) k aféliu (r_a) a potom opäť k perihéliu by sa mala hlavná poloos eliptickej dráhy pootočiť v smere obehu planéty o uhol Dj , pre ktorý platí:

^ra

Dj = 2. ò L / r². [ 2m( E – U_r ) – L²/r² ]^1/2 .dr (X₉)

_rp

r_p, r_a - aféliová a perihéliová hranica

L- moment hybnosti planéty v aféliu a perihéliu

U_r – polohová energia planéty v aféliu a perihéliu

Ak by výpočet integrálu z rovnice (X₉) potvrdil náš predpoklad, potom uhol Dj by mal byť väčší ako 2p a išlo by o otáčanie perihélia planét v smere ich obehu okolo centrálneho telesa.

Od radiálnej rýchlosti vzhľadom na sústavu S môžeme odvodiť zložku Coriolisovej sily, ktorej umiestnením je normálová zložka rýchlosti.Od normálovej zložky rýchlosti odvodíme druhú zložku Coriolisovej sily, ktorej umiestnením je vektor a_o (obr.č. 6), ale má opačnú orientáciu. Keďže dostredivá sila je reprezentovaná normálovou zložkou Coriolisovej sily môžeme napísať rovnicu:

F_(cn) = F_(d)

w × ( w × r ) = w × v_n

w.a_o = v_n, z ktorej môžeme určiť normálovú zložku rýchlosti

v_n = w . a_o = w .r . cos a (30)

Dostredivou silou je tiež gravitačná sila, ktorá je ale radiálna a preto by mala platiť aj nasledujúca rovnica:

F_d = F_g .cos a

mw ²a_o = GMm / r ² . cos a

mw ²r cos a = GMm / r ² . cos a

Po úprave bude pre uhlovú rýchlosť planéty platiť rovnica:

(31)

Ak rovnicu (31) dosadíme do (30),môžeme z nej vyjadriť veľkosť normálovej zložky rýchlosti planéty pri jej obehu okolo Slnka:

(32)

Pretože trajektória planéty je elipsa, vzdialenosť r planéty od Slnka určíme v polárnych súradniciach rovnicou:

(33)

kde p- je parameter dráhy, pre ktorý platí: p = b² / a - a , b je dĺžka hlavnej a vedľajšej poloosi,

e- numerická excentricita daná výrazom: e = e / a, kde e- je lineárna excentricita (vzdialenosť ohniska od stredu elipsy), pre ktorú platí: e = (a² – b²)^1/2

φ- uhlová vzdialenosť planéty od perihélia

Vzdialenosť planéty potom vyjadríme rovnicou:

(34)

Po dosadení za w , a , r do rovnice (29) odvodíme pre moment hybnosti planéty na svojej trajektórii rovnicu:

L = m.( GM_s r )^1/2. cos ² a (35)

M_s- hmotnosť Slnka

m- hmotnosť planéty

r- vzdialenosť planéty od Slnka

Z rovnice (35) môžeme vypočítať moment hybnosti pre ľubovolnú uhlovú vzdialenosť planéty j od perihélia. Pre aféliovú vzdialenosť možno výpočtom získať tieto hodnoty: L=2,687.10 ⁴⁰ kg m ²s ^-1 ; rýchlosť planéty v aféliu nadobúda hodnotu v_n= 29,54. km.s ^-1 a uhlová rýchlosť hodnotu w =1,942.10 ^–7 rad.s ^-1 . Pre perihéliovú vzdialenosť dostaneme nasledovné hodnoty: L = 2,642.10 ⁴⁰ kg m ²s ^-1 , v_n= 30,04. km.s ^–1 , w = 2,042.10 ^–7 rad.s ^–1. Pri výpočte momentu hybnosti L podľa rovnice (35) platí, že sa číselne rovný momentu hybnosti L_s hmotného bodu s hmotnosťou planéty, ktorý rotuje okolo Slnka s periódou číselne rovnou siderickej obežnej dobe planéty T_S podľa rovnice

L = L_s

Napríklad pre afélium bude platiť: m.( GM_s r )^1/2. cos ² a = m r ². 2p / T_s

L = 2,687.10 ⁴⁰ kg m ²s ^–1

L_s = 2,687.10 ⁴⁰ kg m ²s ^-1

L_s- moment hybnosti hmotného bodu so siderickou dobou obehu

L- moment hybnosti planéty určený z rovnice (35)

T_s-siderická doba obehu planéty(Zeme)

Na záver tejto kapitoly by sme mali čitatateľa tejto práce upozorniť na niektoré zaujímavosti, ktoré súvisia s našou teóriou. Výpočtom sa možno presvedčiť, že moment hybnosti planéty podľa rovnice (35) v perihéliu je menší než v aféliu. Čo to ale značí? Ak sa moment hybnosti mení, musí existovať podľa druhej vety impulzovej vonkajšia sila, ktorá túto zmenu spôsobuje. Jej pôvod treba hľadať v už spomínanom rotujúcom gravitačnom poli. V našom prípade by mohlo ísť o otáčanie perihélia planéty v smere jej pohybu. Ďalší dôležitý jav, ktorý tiež súvisí s druhou vetou impulzovou je existencia štyroch točivých momentov, ktoré sa uplatňujú aj pri opise vzniku vesmíru aj pri pohybe planét-rovnica (X₀) v kapitole Coriolisova sila. Točivé momenty, ktoré spolu súvisia v danom bode trajektórie s radiálnou zložkou Coriolisovej sily F_cr a so zložkami sily súvisiacimi s radiálnym spomalením F_r a s uhlovým spomalením F_e, alebo s ich zrýchlením pri pohybe od afelia k perihéliu ležia na jednej priamke, ale majú vždy opačnú orientáciu smeru. Pri pohybe planét sú zodpovedné za zrýchlený a spomalený pohyb po rovine ekliptiky. Štvrtý točivý moment, ktorý súvisí s dostredivou silou F_cn zodpovedá spolu s predchádzajúcimi momentami za to, že rovina ekliptiky sa vzhľadom na rovinu gravitačného rotačného poľa centrálneho telesa (slnečného rovníka) nemení a ak sa mení, potom sa podľa tohto opisu bude meniť vzhľadom na stálice tak, ako sa bude v priestore meniť smer rotačnej osi centrálneho telesa ,okolo ktorého sa planéta pohybuje.

V rovnici (35) vystupuje kvadrát goniometrickej funkcia kosinus. Ak by bol tento uhol, ktorý zviera vektor uhlovej rýchlosti rotujúceho gravitačného poľa centrálneho telesa s vektorom dráhovej uhlovej rýchlosti satelitu rovný p/2, potom by musel byť moment hybnosti takéhoto telesa rovný nule,čo by bol fyzikálny paradox. Čo to znamená? Stabilné usadenie satelitu na polárnu orbitálnu dráhu bez korekčných motorov, ktoré by kompenzovali Coriolisovu silu je fyzikálne neuskutočnitelný experiment. Môžeme sa o tom presvedčiť na plánovanom experimente NASA, ktorý má uskutočniť kozmická sonda Mars Odyssey (Kozmos, 2001/3) a ktorá má začať obiehať okolo Marsu v októbri roku 2001(v súčasnosti je to už minulosť; podľa: mars. discovery @ seznam.cz k 31.01.2002 sú parametre orbity Mars Odyssey nasledovné: inklinácia k rovníku 93.0^o, doba obehu T = 118.2 min, pericentrum = apocentrum = 400 km.). Ak spomínaný experiment nepotvrdil našu argumentáciu, je všetko inak? Určite nie, pretože Newtonova modifikovaná dynamika gravitačnej interakcie jasne hovorí, že na polárnu trajektóriu nemožno umiestniť žiaden satelit a kruhová trajektória s inklináciou i=93^o je podľa rovnice (X_o) fyzikálne nerealizovatelná, ale eliptická áno.