2.1 Definícia ťažiska troch hmotných bodov :

Je to bod na spojnici prvých dvoch hmotných bodov a bodu tretieho, ktorý delí túto spojnicu v obrátenom pomere súčtu hmotnosti prvých dvoch hmotných bodov a bodu tretieho.

Polohový vektor ťažiska troch hmotných bodov :

Nezáleží teda na tom, ktoré dva body z troch daných zvolíme za prvé dva.

Pre súradnice ťažiska platí :

, kde x_i je súradnica í- teho bodu

, kde y_i je súradnica í- teho bodu

, kde z_i je súradnica í- teho bodu

Poloha ťažiska telesa spojite vyplneného hmotnosťou sa určí objemovou integráciou:

,kde s je merná hmotnosť telesa, ktorá vo všeobecnosti v rôznych bodoch telesa je rôzna. Keď je však rovnaká, môžeme písať :

,kde V je objem telesa.

Ak máme dve telesá s hmotnosťami M₁ a M₂ a polohové vektory ich ťažísk sú r₁^* a r₂^*, potom pre ťažisko telies ako jediného celku platí:

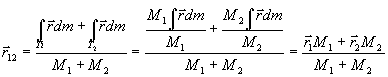
Podľa tohto výsledku spoločné ťažisko dvoch (alebo aj väčšieho počtu) telies nájdeme tak, že dané telesá nahradíme hmotnými bodmi s rovnakými hmotnosťami v ťažiskách jednotlivých telies.