




1.3 Vektorová funkcia a jej derivácie
Základnými charakteristikami vektorových veličín sú ich veľkosť a smer. Tieto charakteristiky môžu závisieť od času, prípadne od priestorových súradníc, podobne ako pri skalárnych veličinách. Napríklad teplota v miestnosti sa môže meniť s plynúcim časom, ráno je iná ako popoludní, ale vo väčšej miestnosti v rovnakom čase nemusí byť teplota v rôznych miestach rovnaká. Podobné závislosti sú možné aj pri vektorových veličinách. Napríklad rýchlosť prúdenia vody v rieke v pevne zvolenom bode koryta vo všeobecnosti sa s časom mení, závisí od vodného stavu. A istotne v danom časovom okamihu v rôznych miestach rieky je rýchlosť rôzna - nie iba čo do veľkosti, ale aj čo do smeru.
Preto možno hovoriť o vektorových funkciách viacer ých premenných, špeciálne priestorových súradníc x, y, z a času t . Túto skutočnosť vyjadrujeme zápisom f (x,y,z,t) . Každá vektorová funkcia má v trojrozmernom priestore vo všeobecnosti tri zložky, pričom každá zložka opäť závisí od priestorových, aj od časovej súradnice. Preto funkciu f
pomocou zložiek zapíšeme v tvare
f (x,y,z,t) = fx (x,y,z,t) i + fy (x,y,z,t) j + fz (x,y,z,t) k (1.3.1)
Špeciálnym prípadom je vektorová funkcia, ktorá závisí len od času : f(t) . Je to funkcia, pri ktorej s plynúcim časom sa môže meniť jej veľkosť i smer. V súlade s vyjadrením podľa (1.3.1) má tri zložky, pričom vo zvolenej súradnicovej sústave každá z jej súradníc závisí od času, nie však od priestorových súradníc. Vhodným príkladom je polohový vektor pohybujúcej sa častice r (t) , ktorý spája začiatok
súradnicovej sústavy s časticou, takže koniec vektora sa posúva po krivke, po
ktorej sa častica pohybuje :
r (t) = x(t) i + y (t) j + z(t) k .
Príkladom vektorovej funkcie závisiacej od priestorových súradníc, ale nemeniacej sa s časom, je vektor intenzity E v elektrostatickom poli bodového náboja. Túto jeho závislosť vyjadrujeme zápisom E (x,y,z) .
Pri opise fyzikálnych dejov, alebo polí, nestačí poznať len hodnoty funkcií, ale aj ich zmeny, či už súvisiace s plynúcim časom, alebo zmeny pozdĺž jednotlivých priestorových súradníc. Na tento účel slúžia derivácie vektorových funkcií.
Derivácia vektorovej funkcie závisiacej od času.
Zavádza sa rovnako, ako derivácia funkcie jednej premennej, t.j. ako limita podielu. Napríklad derivácia polohového vektora r (t) sa definuje vzťahom: 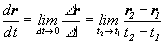
(1.3.2)
kde r1 a r2 sú polohové vektory (napr. pohybujúcej sa častice) v okamihoch t1 a t2 . Takto je definovaná okamžitá rýchlosť (častice), pomocou ktorej možno dobre pochopiť význam derivácie vektorovej funkcie. Na obrázku 1.3.1 sú nakreslené príslušné vektory, takže vidno smer i veľkosť vektora D
r . V limite pri t2 ®
t1 sa vektor r2 približuje k vektoru r1 , 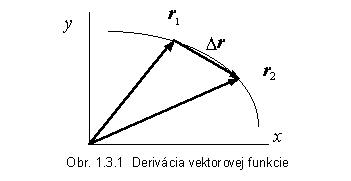
takže vektor D
r sa skracuje a postupne sa svojim smerom približuje ku smeru dotyčnice krivky v bode s polohovým vektorom r1 . V definícii derivácie v menovateli zlomku vystupuje časový interval, teda skalárna veličina, takže podiel D
r/D
t je v podstate skalárnym násobkom vektora D
r , pričom násobiacim skalárom je zlomok 1/D
t. Preto výsledkom derivácie vektorovej funkcie podľa času je opäť vektorová funkcia, ktorej smer je určený čitateľom zlomku z definície derivácie. V tomto prípade smer vektora rýchlosti je totožný so smerom dotyčnice krivky v bode r1 . Veľkosť výsledku predstavuje
veľkosť okamžitej rýchlosti (častice).
Pri konkrétnych výpočtoch derivácie vektorovej funkcie, keď chceme získať číselné hodnoty, treba vektorovú funkciu vyjadriť v zložkách, ako v (1.3.1). Napríklad polohový vektor pohybujúcej sa č astice má potom tvar : r (t) = x(t) i + y (t) j + z(t) k
. Takto zapísaná vektorová funkcia predstavuje súčet troch funkcií, preto
deriváciu polohového vektora vyjadríme ako súčet derivácií jeho troch zložiek
: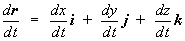
(1.3.3)
V tomto výraze vystupujú zložky rýchlosti : vx i = (dx/dt) i atď. resp. súradnice vektora rýchlosti vx = (dx/dt) .
Súradnica vektora rýchlosti predstvuje zmenu príslušnej súradnice polohového
vektora pripadajúcej na jednotkový časový interval. Podľa definície derivácie
platí 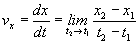
(1.3.4)
Táto derivácia môže byť kladná, i záporná (pravdaže i nulová). Kladná je vtedy, keď s pribúdajúcim časom rastie hodnota súradnice, záporná v opačnom prípade.
Význam "zlomku" dx/dt pochopíme na základe nasledujúcej úvahy. Ak častica za 1 s prejde napríklad 5 m, tak číselnú hodnotu rýchlosti častice vyjadríme ako podiel 5/1 = 5 . Táto častica za časový interval 0,1 s prejde 0,5 m , za 0,01 s 0,05 m atď. , ale podiel hodnôt 0,5/0,1 = 0,05/0,01 … atď. je stále rovnaký a zachová sa aj v limitnom prípade, keď hodnota menovateľa t2 - t1 sa blíži k nule. Preto výraz dx/dt vyjadruje zmenu súradnice pripadajúcu na jednotkový časový interval (sekundu). Takto treba chápať význam derivácie aj v iných prípadoch, keď v čitateli i v menovateli limity (1.3.4) sú iné premenné ako v tomto uvedenom príklade.
Príklad 1.3.1 Vypočítajte súradnice, zložky a veľkosť rýchlosti častice, keď súradnice jej polohového vektora sú vyjadrené takto : x =
p t , y = q + st + 0,5 ut 2 , z = 0, pričom konštanty vo vzorcoch majú hodnoty p = -3 m/s , q = 4 m , s = 2 m/s , u = - 9,81 m×
s-2 .
Riešenie : Ak orientujeme os x vodorovne a os y zvislo, tak pozornejší čitateľ zistí, že ide o šikmý vrh, zo začiatočnej výšky q = 4 m , začiatočnou rýchlosťou s = 2 m/s nahor a rýchlosťou p = 3 m/s vodorovne v zápornom smere osi x . Vyjadríme polohový vektor v zložkovom tvare : r(t) = pt i + (q + st + 0,5 ut2 ) j + 0 k . Vektor rýchlosti získame deriváciou polohového
vektora, pričom použijeme vzorec (1.3.2) :
v = p i + (s + ut ) j ,
kde vidno dve zložky vektora v - zložku v smere vektora i a zložku v smere vektora j . Pre súradnice vektora v pritom platí : vx =
p = -3 m/s , vy = s + ut = (2 - 9,81 t ) m/s . To znamená, že súradnica vy sa mení s časom. Jej konkrétna číselná hodnota závisí od časového údaja, ktorý do vťahu pre súradnicu dosadíme. Veľkosť vektora v získame, ak použijeme vzorec (1.1.6) : v = [
p2 + (s + ut )2] 1/2
Derivácie súčinov vektorových funkcií
Vektorová funkcia môže byť výsledkom
skalárneho násobku inej vektorovej funkcie, pričom vo všeobecnom prípade
skalárna, aj pôvodná vektorová funkcia môžu závisieť od času. Napríklad ak
b(t) = s(t) a(t) , potom pri derivácii tohoto výrazu musíme postupovať ako pri derivácii súčinu :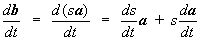 (1.3.5)
Podobne, ak máme derivovať skalárny, alebo vektorový súčin dvoch vektorových funkcií závisiacich od času, treba postupovať podľa pravidla pre deriváciu súčinu : 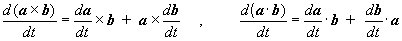
(1.3.6)
Pri derivácii vektorového súčinu treba zachovať poradie vektorových funkcií, pri skalárnom súčine možno uplatniť jeho komutatívnosť. Analogicky postupujeme, ak máme derivovať napríklad skalárny násobok vektorového súčinu s(a ´
b) , alebo súčin skalárnej funkcie so skalárnyn súčinom s(a ×
b) .
Príklad 1.3.2 Derivujte podľa času vektorovú funkciu F(t), ktorá
je výsledkom násobenia vektorovej funkcie skalárnou funkciou času, F(t) = (3t 2) (p i + qt j + rt 2 k) , kde p, q, r sú konštanty. Vypočítajte veľkosť výsledného vektora G(t ) v čase t = t1 .
Riešenie : Postupujeme podľa vzorca (1.3.4) :
dF/dt = (6t ) (p i + qt j + rt 2 k) + (3t 2) (q j + 2rt k) = 6pt i + (6qt 2 + 3qt 2) j + (6rt 3 + 6rt 3)k Veľkosť výsledného vektora G(t ) = 6pt i + 9qt 2 j + 12rt 3k vypočítame podľa vzťahu (1.1.6), do ktorého dosadíme konkrétny časový údaj t1 :
G(t) = [
(6pt1)2 + (9qt12)2 + (12rt13)2 ]
1/2 .
Derivácia skalárnej funkcie podľa priestorových premenných, gradient
Nech je v karteziánskej súradnicovej sústave zadaná skalárna funkcia P(x,y,z), napríklad elektrostatický potenciál. Hodnoty tejto funkcie sa menia, ak postupujeme v smere jednotlivých súradnicových osí, pričom stromosť zmeny nemusí byť vo všetkých smeroch rovnaká. Pod strmosťou zmeny rozumieme prírastok hodnoty funkcie pripadajúci na posunutie v príslušnom smere o jednotku dĺžky (1 meter). Strmosti v smere osí x, y, z označíme symbolmi Sx , Sy , Sz pričom pre ne platí 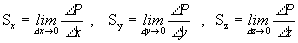 (1.3.7)
Limity vo výrazoch pre strmosť predstavujú derivácie. Pri posunutí pozdĺž osi y sa mení len súradnica y , ostatné dve zostávajú nemenné. Takáto derivácia funkcie viacerých premenných sa nazýva parciálna a označuje sa inak ako derivácia funkcie jednej premennej. Strmosť zmien funkcie P(x,y,z) sa vyjadruje potom v tvare :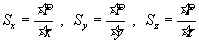
(1.3.8)
Strmosti Sx , Sy , Sz nie sú v celom priestore konštantné, ale sa môžu od bodu k bodu meniť. Ak postúpime v smere osi y o D
y , zmení sa hodnota funkcie P(x,y,z) o hodnotu :
(D
P)y = Sy D
y = (¶
P/¶
y) D
y . (1.3.9)
Ak vykonáme posunutie všeobecným smerom, možno ho rozložiť na tri posunutia v smeroch súradnicových osí, takže celková zmena funkcie P(x,y,z) bude
D
P = (D
P)x + (D
P)y + (D
P)z = (¶
P/¶
x) D
x + (¶
P/¶
y) D
y + (¶
P/¶
z) D
z (1.3.10)
alebo pri limitne malých posunutiach :
dP = (¶
P/¶
x) dx + (¶
P/¶
y) dy + (¶
P/¶
z) dz (1.3.11)
Takýmto vzťahom je vyjadrený úplný (totálny) diferenciál funkcie troch priestorových premenných. Vzťah (1.3.11) možno vyjadriť
ako skalárny súčin dvoch vektorov :
diferenciálu polohového vektora
dr = dx i + dy j + dz k (1.3.12)
a vektora, ktorý nazývame gradient skalárnej funkcie P :
grad P(x,y,z) = (¶
P/¶
x) i + (¶
P/¶
y) j + (¶
P/¶
z) k (1.3.13)
O správnosti tohoto tvrdenia sa čitateľ môže presvedčiť vykonaním skalárneho súčinu.
Vektor grad P má smer najstrmšieho vzrastu funkcie P a jeho veľkosť sa rovná tomuto vzrastu, t.j. prírastku funkcie P pripadajúcemu na posunutie o jednotku vzdialenosti. Na ilustráciu - v danom mieste mapy by tento vektor bol kolmý na vrstevnice a veľkosťou by predstavoval prírastok nadmorskej výšky pri posunutí o jednotku vzdialenosti v príslušnom horizontálnom smere.
Výraz grad P sa zapisuje v symbolickom tvare :
grad P = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) P , (1.3.14)
pričom výraz v zátvorke predstavuje diferenciálno - vektorový operátor, nazývaný nabla operátor a označovaný symbolom N
:
N
= ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) (1.3.15)
Jeho aplikáciou na skalárnu funkciu podľa vzoru (1.3.13) vznikne zo skalárnej funkcie vektorová funkcia. Aplikovať operátor znamená vykonať operácie, ktoré predpisuje. To znamená, že podľa vzťahu (1.3.14) treba skalárnu funkciu najprv parciálne derivovať podľa premennej x a týmto výsledkom (skalárom) násobiť jednotkový vektor i . K tomuto členu - prvej zložke výsledného vektora - pripočítať druhý a tretí člen, ktoré dostaneme analogicky, deriváciami podľa premenných y a z , ktorými vynásobíme jednotkové vektory j a k .
Príklad 1.3.3 Vypočítajte gradient skalárneho elektrostatického potenciálu v okolí bodového náboja Q , umiestneného v začiatku súradnicovej sústavy. Potenciál je vyjadrený vzťahom V(x,y,z) = K (x2 + y2 + z2)-1/2 , kde K = (Q / 4p
e
o).
Riešenie : Najprv vypočítame parciálnu deriváciu potenciálu podľa premennej x :
¶
P/¶
x = K (-1/2)(x2 + y2 + z2)-3/2 (2x) = - K x (x2 + y2 + z2)-3/2 . Výsledky parciálnych derivácií podľa premenných y a z sú analogické, takže môžeme priamo napísať grad V , keď k výsledkom derivácií dopíšeme jednotkové vektory : 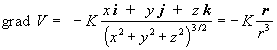 (1.3.16)
kde r = xi + yj + zk je polohový vektor miesta v ktorom počítame vektor grad V a v menovateli je tretia mocnina veľkosti polohového vektora. Vektor grad V má opačný smer ako polohový vektor r , lebo elektrostatický potenciál s rastúcou vzdialenosťou od náboja klesá, takže smer vzrastu potenciálu, a teda vektora grad V
je opačný.
Gradient vektorovej funkcie predstavuje aplikáciu nabla operátora na vektorovú funkciu. Napríklad grad B(x,y,z) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) B = i ¶
B/¶
x + j ¶
B/¶ y + k ¶
B/¶
z ,
pričom len výraz j ¶
B/¶ y = j ( ¶
Bx / ¶
y i + ¶
By /¶
y j + ¶
Bz /¶
y k ) obsahuje tri členy. Spolu v celom grad B je deväť členov v ktorých však vťahy medzi vystupujúcimi vektormi sme zatiaľ nedefinovali. Ide o t.zv. tenzorovú veličinu, ktorej v tomto texte ďalšiu pozornosť nevenujeme .
Pri opise fyzikálnych polí sa často stretávame s výrazmi, ktoré možno formálne vyjadriť ako skalárny, alebo ako vektorový súčin nabla operátora s vektorovou funkciou. Označujú sa názvami divergencia, resp. rotácia vektorovej funkcie.
Divergencia vektorovej funkcie sa zavádza vzťahom :
div F(x,y,z) = N
×
F = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ×
(Fx i + Fy j + Fz k ) =
= ¶
Fx /¶
x + ¶
Fy /¶
y + ¶
Fz /¶
z (1.3.17)
V symbolickom skalárnom súčine nabla operátora s vektorovou funkciou sa postupuje rovnako, ako pri skalárnom súčine dvoch vektorových funkcií, zapísaných v zložkovom tvare, teda podľa vzorca (1.2.5). Výsledkom divergencie vektorovej funkcie je skalárna funkcia. Súčin je skutočne symbolický, lebo nabla operátor nie je v skutočnosti vektor, nemožno hovoriť o jeho veľkosti, ani o smere.
Rotácia vektorovej funkcie sa zavádza vzťahom :
rot F(x,y,z) = N
´
F = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ´
(Fx i + Fy j + Fz k ) = 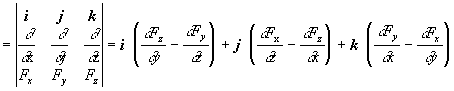
Aj v tomto prípade sa symbolický vektorový súčin nabla operátora s vektorovou funkciou počíta podľa pravidiel vektorového súčinu medzi vektormi vyjadrenými v zložkách, teda podľa vzorcov (1. 2.16)
a (1.2.17) .
Príklad 1.3.4 Vypočítajte divergenciu a rotáciu vektorovej funkcie f = r(x,y,z) = xi + yj + zk . Uvedomte si, že takáto funkcia (polohový vektor) má charakter radiálneho vektorového poľa, keď v ľubovoľnom bode priestoru tejto funcii prislúcha vektor r
smerujúci od stredu (začiatku) súradnicovej sústavy (obr. 1.3.2)Riešenie : div r = = ¶
x /¶
x + ¶
y /¶
y + ¶
z /¶
z = 3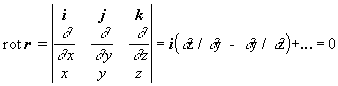
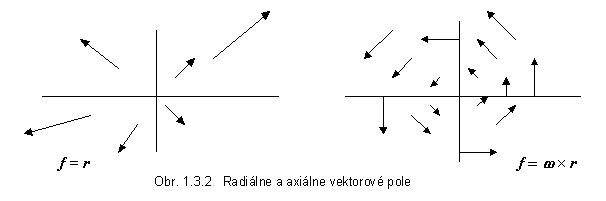
Príklad 1.3.5 Vypočítajte divergenciu a rotáciu vektorovej funkcie f (x,y,z) = w
´
r ktorá je vektorovým súčinom konštantného vektora w
s polohovým vektorom r . Nech r = x i + y j a w =
w
k . Vektorová funkcia f zobrazuje pole vektora rýchlosti pri otáčaní roviny uhlovou rýchlosťou w . Je to
príklad axiálneho vektorového poľa, v ktorom vektorová funkcia má vždy smer
dotyčnice ku kružnici, ktorej stred leží v začiatku súradnicovej sústavy.
Riešenie : Najprv vypočítame vektorový súčin w
´
r = (w
k) ´
(xi + yj) = xw
j -
y w
i . Potom
div f = N
×
f = N
×
( w
´
r ) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ×
(xw
j -
y w
i ) = 0
rot f = N
´
f = N
´
( w
´
r ) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ´
(xw
j -
y w
i ) = 2w
k
Výsledky príkladov 1.3.4 a 1.3.5 hovoria o tom, že rotácia vektorovej funkcie predstavujúcej radiálne pole sa rovná nule, ale rotácia v prípade axiálneho poľa je nenulová. Naopak je to pri divergencii, kde nenulový výsledok sme dostali pri radiálnom poli. Tieto výsledky naznačujú význam o perácií divergencia a rotácia pri charakterizácii fyzikálnych polí. Elektrostatické pole v okolí bodového náboja má radiálny charakter, zatiaľ čo magnetické pole v okolí vodičov elektrického prúdu charakter axiálny. Táto vlastnosť sa odzrkadľuje aj na Maxwellových rovniciach, keď pre vektor intenzity el. poľa vo vákuu platí div E = r
/e
o ale pre vektor magnetickej indukcie div B = 0 . A naopak , v elektrostatickom poli platí rot E =
0 , ale pre vektor intenzity stacionárneho magnetického poľa platí rot H = j , kde j je vektor prúdovej hustoty.
Dvojnásobné použitie nabla operátora Doteraz uvedené aplikácie operátora nabla
predstavujú prvé derivácie funkcií priestorových premenných. Operátor však možno
aplikovať na funkciu získanú prvou deriváciou, čím vznikajú druhé derivácie funkcií. Operátor možno na funkcie aplikovať zase tromi spôsobmi (ako gradient, divergenciu a rotáciu), preto jestvuje aj viac prípadov druhých derivácií.
Najprv uvedieme všetky možnosti druhej derivácie skalárnej funkcie S(x,y,z) :
a) N
×
(N
S) = div grad S(x,y,z) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ×
( i ¶
S/¶
x + j ¶
S/¶
y + k ¶
S/¶
z) =
= ( ¶
2S /¶
x2 + ¶
2S /¶
y2 + ¶
2S /¶
z2) = D
S ,
kde D
= N
×
N
= N
2 = ( ¶
2/¶
x2 + ¶
2/¶
y2 + ¶
2/¶
z2) je Laplaceov operátor.
Výsledkom tejto druhej derivácie je skalárna funkcia, čo v podstate vidno hneď na začiatku, kde ide o symbolický skalárny súčin.
N
×
(N
S) = D
S (1.3.19)
b) N
´
(N
S) = rot grad S(x,y,z) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) ´
( i ¶
S/¶
x + j ¶
S/¶
y + k ¶
S/¶
z) =
= i ( ¶
2S /¶
z¶
y - ¶
2S /¶
y¶
z) + j (¶
2S /¶
z¶
x - ¶
2S / ¶
x¶
z) + k (¶
2S /¶
x¶
y - ¶
2S /¶
y¶
x) = 0
Rotácia gradientu skalárnej funkcie sa vždy rovná nule :
N
´
(N
S) =
0 (1.3.20)
c) Tretia možnosť - N
(N
S) = grad grad S by
predstvavovala tenzorovú veličinu, ale s takýmto prípadom druhej derivácie sa
pri opise fyzikálnych polí prakticky nestretávame.
Druhé derivácie vektorových funkcií :
d) N
(N
×
A) = grad div A(x,y,z) = ( i ¶
/¶
x + j ¶
/¶
y + k ¶
/¶
z) (¶
Ax /¶
x + ¶
Ay /¶
y + ¶
Az /¶
z)
= i (¶
2Ax /¶
x2 + ¶
2Ay /¶
y¶
x + ¶
2Az /¶
z¶
x) + j (¶
2Ax /¶
x¶
y + ¶
2Ay /¶
y2 + ¶
2Az /¶
z¶
y ) +
+ k (¶
2Ax /¶
x¶
z + ¶
2Ay /¶
y/¶
z + ¶
2Az /¶
z2 )
Výsledkom je vektorová funkcia. Operáciou v zátvorke (N
×
A) vzniká z vektorovej funkcie skalárna funkcia, ale nasledujúci gradient z nej opäť vytvorí vektorovú funkciu. e) Druhú deriváciu N
×
(N
´
A) = div rot A(x,y,z) možno vyjadriť podobne ako zmiešaný súčin v tvare determinantu (vzťah 1.2.22). Vidno, že v determinante sú dva riadky rovnaké, pozostávajúce zo "súradníc " nabla operátora, takže po realizácii celého výpočtu získame dvojice rovnakých členov s opačnými znamienkami. Preto je výsledok tejto druhej derivácie vždy nulový :N
×
(N
´
A) = 0 (1.3.21)
f) Druhú deriváciu N
´
(N
´
A) = rot rot A(x,y,z) rozpíšeme podľa predpisu pre dvojnásobný súčin : N
´
(N
´
A) = N
( N
×
A) - (N
×
N
)A = grad div A - div grad A = grad div A - D
A (1.3.22)
Uvedené druhé derivácie sa používajú pri formuláciách zákonov platných vo fyzikálnych poliach. Riešenie príkladov obsahujúcich tieto derivácie neuvádzame.
Kontrolné otázky k časti 1.3
Definujte, čo je skalárna a čo vektorová funkcia
viacerých premenných !
Ak vektorová funkcia závisí od viacerých
premenných, závisia od nich aj jej zložky (súradnice) ?
Uveďte príklad vektorovej funkcie, ktorá
závisí len od času !
Uveďte príklad vektorovej funkcie, ktorá
závisí len od priestorových súradníc !
Vyjadrite, čo rozumieme pod deriváciou
vektorovej funkcie podľa času !
Výsledkom derivácie vektorovej funkcie podľa
času je funkcia vektorová, alebo skalárna ?
Slovne vyjadrite, čo predstavuje veľkosť
derivácie vektorovej funkcie podľa času ?
Vyjadruje derivácia vektorovej funkcie podľa
času aj smer výslednej vektorovej funkcie ?
Ako derivujeme podľa času súčin vektorovej a
skalárnej funkcie (t.j. skalárny násobok vekt. funkcie), keď obe funkcie
závisia iba od času ?
Vyjadrite deriváciu skalárneho súčinu dvoch
vektorov podľa času !
Vyjadrite deriváciu vektorového súčinu dvoch
vektorov podľa času !
Vyjadrite totálny diferenciál funkcie
priestorových premenných x, y, z !
Uveďte, čo je gradient skalárnej funkcie
priestorových premenných !
Čo predstavujú súradnice (zložky) gradientu
skalárnej funkcie ?
Napíšte nabla operátor ! Je to skutočný
vektor ? Má veľkosť a smer ?
Uveďte, čo rozumieme pod divergenciou
vektorovej funkcie !
Uveďte, čo rozumieme pod rotáciou vektorovej
funkcie !
Napíšte rotáciu vektorovej funkcie v tvare
determinatu !
Uveďte charakteristiky radiálneho a axiálneho
vektorového poľa - aká je ich divergencia a rotácia !
Uveďte niektoré operácie s dvojnásobným
použitím nabla operátora (t.j. druhé derivácie)!
Uveďte aspoň jeden prípad dvojnásobného
použitia nabla operátora , v ktorom je výsledok vždy nulový !
|