THE ACOUSTIC ATTENUATION THEORETICAL MODELS FOR THE ION CONDUCTIVE GLASSES

 

P. Hockicko(1) , S. Jurečka(2) , P. Bury(1) , M. Jamnický(3) , I. Jamnický(1)

(1)Departmentof Physics, Faculty of Electrical Engineering, University of Žilina, Veľký Diel, 010 26 Žilina, Slovak Republic

(2)Departmentof Engineering Fundamentals, Faculty of Electrical Engineering, University of Žilina,kpt. J. Nálepku 1390, 031 01 Liptovský Mikuláš

 (3)Department of Ceramic, Glass and Cement, Faculty of Chemical and Food Technology, Slovak University of Technology, Radlinského 9, 812 37 Bratislava

e-mail: hockicko@fyzika.utc.sk

 

Introduction

The experimental study of transport mechanisms in glassy electrolytes with fast ion transport attracts the considerable interest for its important role in a number of modern electrochemical devices. Acoustical measurements can characterize different relaxation processes in the ion conductive glasses and seem to be a useful technique for nondestructive investigation of transport mechanisms in conductive glasses even with some advantages compared to the electrical measurements. The distinctive peaks of acoustic attenuation spectra which are caused by resonant interaction with the mobile ion hopping processes enable us then to study relaxation and transport mechanisms in the ion conductive glasses.

Phosphate glasses containing Cu+ conductive ions are good ionic conductors with room temperature conductivity of the order 10-3 W-1cm-1 and the highest conductivity has been recorded in systems containing large fractions of cuprous halides, such as CuI or CuBr [1]. The investigation of acoustic spectra in ion conductive glasses with different composition can reflect the basic features of the relaxation and transport processes of the mobile ions.It was found that the temperature responses of all acoustic spectra are similar and the relaxation peaks associated with ion transport depend on the glass composition.

 In this contribution we present an analysis of the acoustical spectra using various theoretical models for the simulations to fit the experimental data of representative samples of phosphate glasses containing Cu+ conductive ions in the system CuI-CuBr-Cu2O-P2O5 with the purpose to study the ion transport mechanisms in these fast ion conductive glasses.

 

Theory

The ion transport properties and the formal theories of all relaxation processes of many ion conducting glasses, melts and crystals are similar [2]. In dilute system containing a low concentration of mobile ions the attenuation may be described as a Debye-like, single relaxation time processes in which the individual ion hops occur independently of each other. In such cases, the attenuation a for a wave of angular frequency w takes the form [3]

 

  ,

(1)

where the parameter D is the relaxation strength, , that determines the magnitude of the attenuation peak. Here N is the number of mobile ions, B is the deformation potential, r is the density of the solid, v is the velocity of the sound wave, kB is the Boltzmann constantand T is the absolute temperature.

The term in equation (1) in the round brackets describes a Debye peak. The acoustic attenuation will exhibit a maximum when the relaxation time tis comparable to the period (1/w) of the acoustic perturbation and the condition wt  = 1 is fulfilled, where [4]

 

(2)

is the most probable relaxation time. The relaxation processes described by the Arrhenius equation (2) are characterized by the activation energy EA for jumps over the barrier between two potential minima and typical relaxation frequency of ion hopping 1/t0» 1013 – 1014 s-1.

The relaxation phenomena observed in a wide variety of materials exhibit a power-law type of frequency dependence. The relationship to the Debye behaviour is expressed in the form

 

  ,

(3)

where m and n are power-law exponents, which take values between 0 and 1. When m = 1 and n = 0, Eq. (3) reduces to Eq. (1) for a single Debye-like process [3].

Another function has mainly been used to fit mechanical loss data [5]. This function is the double power law

 

  .

(4)

Using these functions, we can fit also the acoustic attenuation spectrum of the measured cuprous halides glasses. 

 

Experiments and results

The procedure of glasses preparation in the system CuI-CuBr-Cu2O-P2O5 from commercial reagents has been already described [6]. The composition of the complex set of glass samples was summarized in [7]. We tried to fit the measured temperature-dependent acoustic attenuation spectra at constant frequency n= 18 MHz using theoretical models (Eq. 1, 3, 4).

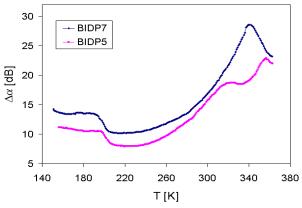
Fig. 1. Temperature dependence of the acoustic attenuation of ion conductive glasses for samples BIDP5 and BIDP7.

 

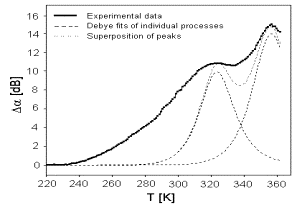
Fig. 2. The acoustic spectrum of sample BIDP5 (full line) and the Debye fit of the two relaxation processes (dashed lines).

 

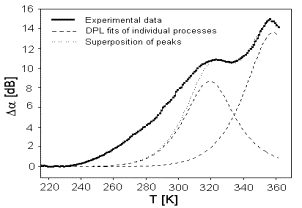
Fig. 3. The acoustic spectrum of sample BIDP5 (full line) and its theoretical supposed fit (spotted line) is superposition of the two supposed relaxation processes (dashed lines).

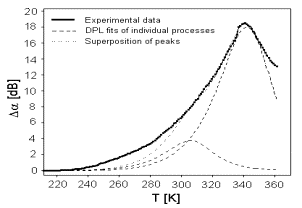
Fig. 4. The acoustic spectrum of sample BIDP7 (full line) and best fit of the two relaxation processes (dashed lines).

 

As we can see, the complete spectrum of sample BIDP5 illustrated in Fig. 2, 3, cannot be fitted supposing only two relaxation processes. The additional third relaxation process should be taken into account with maximum at the temperature around 280 K.

 

Conclusion

The acoustical spectroscopy in connection with suitable relaxation theory seems to be very useful technique for study of transport processes in fast ion conductive glasses. Using the theoretical models the relaxation processes can be described and some ion parameters determined.

The acoustic attenuation spectra of all investigated ion conducting glasses prepared in the system CuI-CuBr-Cu2O-P2O5 consist of more then two thermally activated relaxation processes for temperatures over 220 K. However, the simulation of two processes very well fit the high temperature measured part of the spectra.

The superposition of three loss peaks with different activation energies can better fit the investigated spectrum of the phosphate glasses with various compositions of CuI and CuBr. 

 

Acknowledgement

The authors would like to thank Mr. F. Černobila for technical assistance. This work was partly financially supported by Grant 1/9141/ 02 of the Ministry of Education of the Slovak Republic.

 

References:

 

[1]   P. Znášik, M. Jamnický: Solid State Ionics 95 (1997), 207

[2]   K. Funke, B. Roling, M. Lange: Solid State Ionics 105 (1998), 195

[3]   D. P. Almond, A. R. West: Solid State Ionics 26 (1988), 265

[4]   G. Carini, M. Cutroni, M. Federico, G. Galli, G. Ttipodo:Physical Review B 30 (1984), 7219

[5]   B. Roling, M. D. Ingram: Physical Review B 57 (1998), 14192

[6]   P. Bury, P. Hockicko, M. Jamnický, I. Jamnický: Advances in Electrical and Electronic Engineering, Vol. 2/2003, No. 3-4, 16

[7]   P. Bury, P. Hockicko, M. Jamnický, I. Jamnický: Proc. of the 18th International Congress on Acoustics, Kyoto 2004, (will be published)
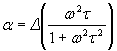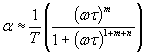