9.5 Kirchhoffove zákony
Preberieme
dôležitý prípad, keď elektrický prúd tečie kovovými vodičmi, rezistormi,
kondenzátormi a cievkami, ktoré vytvárajú tzv. elektrickú sieť. Jednosmerná
sieť, v ktorej tečú časovo ustálené prúdy sa skladá z rezistorov, spojovacích
vodičov a zdrojov jednosmerného elektrického napätia. Tieto prvky sú zapojené
tak, že vytvárajú vetvy (vetva obsahuje spojovacie vodiče, najmenej jeden
rezistor a môže byť v nej zdroj napätia), ktoré sa stretávajú v uzloch (uzol je
spojenie najmenej troch vetiev). Zvyčajne poznáme hodnoty napätí zdrojov a
hodnoty odporov rezistorov. Spojovacie vodiče považujeme za ideálne, t.j.
bezodporové. Úlohou je zistiť výpočtom hodnoty prúdov vo vetvách. Táto úloha sa
rieši pomocou Kirchhoffových zákonov, čo je základná metóda riešenia elektrických
sietí.
Prvý
Kirchhoffov zákon odvodíme z rovnice kontinuity elektrického prúdu pre
stacionárny prípad, ktorého matematické vyjadrenie je (9.4.2). Na obr. 9.5.1 je
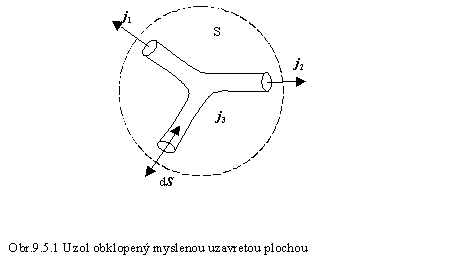
uzol siete, v ktorom sa spájajú vetvy s prúdmi I1, I2, I3. Uzol obklopíme myslenou uzavretou plochou S, ktorá sa skladá z prierezov vodičov (v miestach, kde vodiče
presekávajú túto plochu) S1, S2, S3 a zvyšku S0.
![]()
Vektory dS
a vektory prúdových hustôt j sú
súhlasne alebo nesúhlasne rovnobežné. Skalárne súčiny predstavujú prúdy I1, I2, a -I3.
Posledný integrál sa rovná nule, lebo prúdová hustota je rôzna od nuly len vo
vodičoch. Podľa (9.4.2) je súčet integrálov na pravej strane rovný nule, t.j.
![]()
Všeobecne napíšeme
![]() (9.5.1)
(9.5.1)
kde n
je počet vetiev stretávajúcich sa v uzle. Takže formulácia 1. Kirchhoffovho
zákona znie: Súčet prúdov v uzle sa rovná nule. Musíme rozlišovať znamienkom prúdy, ktoré do
uzla vstupujú od prúdov, ktoré z neho vystupujú. Keďže 1. Kirchhoffov zákon sme
odvodili z rovnice kontinuity, môžeme tiež povedať, že 1. Kirchhoffov zákon je
dôsledkom zákona zachovania náboja.
Druhý
Kirchhoffov zákon odvodíme zo základnej rovnice elektrostatického poľa, ktorá
hovorí, že súčet elektrických napätí dU =
E.dl pozdĺž uzavretej dráhy sa rovná nule. Z Ohmovho zákona v
diferenciálnom tvare j = sE dostaneme
![]()
To znamená, že úbytky napätia dU sa objavujú len tam, kde je prúdová
hustota, t.j. vo vetvách siete. Má teda zmysel voliť si dráhu l pri integrovaní len pozdĺž vetiev, a
to tak, aby sme z vetiev dostali uzavretú dráhu, alebo ako hovoríme, uzavretú
slučku. Pri takejto voľbe budú vektory j
a dl rovnobežné. Potom pre úbytok
napätia na úseku dl v nejakej vetve
môžeme napísať
![]()
kde dR
je odpor rezistora na dĺžke dl. Ak
vezmeme celý rezistor, bude na ňom úbytok napätia U = RI. Na obr. 9.5.2 je časť siete s jednou
uzavretou slučkou a so zvoleným smerom jej
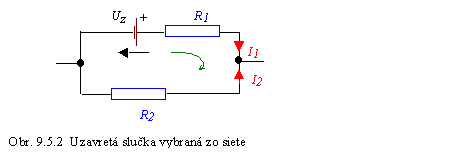
obiehania (t.j. so smerom vektora dl vo vetvách). Pre súčet elektrických
napätí máme
![]()
Okrem napätí na rezistoroch treba uvažovať aj
elektrické napätia zdrojov, pretože aj tieto sa nachádzajú na uzavretej dráhe,
po ktorej integrujeme. Všeobecne môžeme 2. Kirchhoffov zákon napísať
![]() (9.5.2)
(9.5.2)
Súčet
úbytkov napätí vytváraných prúdmi na rezistoroch + súčet elektrických napätí
zdrojov sa v uzavretej slučke rovná nule.
V rovnici (9.5.2) je m počet rezistorov a p
počet zdrojov v slučke.
Pri
riešení sietí je zvykom vyjadrovať sa zjednodušene: aj keď vieme, že elektrický
prúd je skalárna veličina, hovoríme, že v danej vetve tečie prúd nejakým smerom.
V skutočnosti ide o orientáciu vektora prúdovej hustoty j. Z historických dôvodov berieme
orientáciu prúdovej hustoty takú, ako keby nosičmi náboja v kovoch boli kladné
náboje. Takýto smer prúdu nazývame technickým smerom (bol zavedený ešte
pred objavením elektrónu). Pri riešení siete pomocou Kirchhoffových zákonov sa
riadime určitými pravidlami.
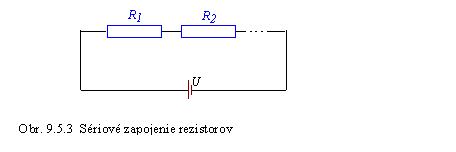
Pri riešení sietí je výhodné sieť zjednodušiť, robíme to tak, že nahrádzame viac rezistorov jedným. Ak máme rezistory zapojené za sebou (do série), obr. 9.5.3, potom odpor náhradného rezistora je
![]() (9.5.3)
(9.5.3)
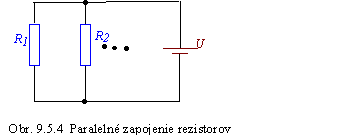
Ak máme rezistory zapojené vedľa seba
(paralelne), obr. 9.5.4, potom odpor náhradného rezistora vypočítame z rovnice
![]() (9.5.4)
(9.5.4)
Pre dva paralelné rezistory je lepšie
používať vzorec
![]() (9.5.4a)
(9.5.4a)
Vyššie uvedené vzorce pre náhradné odpory môžeme odvodiť pre siete na obr. 9.5.3 a obr. 9.5.4 pomocou Kirchhoffových zákonov.
Pri
zjednodušovaní zložitejších sietí sa používa prevod trojuholníka na hviezdu (alebo naopak).
Príklad 9.5.1: Na meranie stredných odporov (100 W až 100 kW) sa používa Wheatstoneov mostík, obr. 9.5.5. Odvoďte podmienku rovnováhy mostíka (mostík je v rovnováhe vtedy, ak nulovým indikátorom neprechádza prúd).
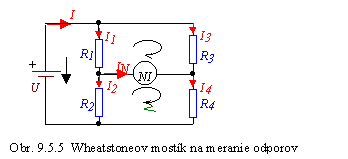
Riešenie: Sieť má 6 vetiev, treba napísať 6 rovníc podľa 1. a 2. Kirchhoffových zákonov. Pri zostavovaní rovníc sa riadime pokynmi. Rovnice podľa 1. Kirchhoffovho zákona:
![]() (a)
(a)
![]() (b)
(b)
![]() (c)
(c)
Rovnice podľa 2. Kirchhoffovho zákona:
![]() (d)
(d)
![]() (e)
(e)
![]() (f)
(f)
Po dosadení podmienky rovnováhy IN = 0 do týchto rovníc sa sústava rovníc zjednoduší a po úpravách a výpočtoch dostaneme podmienku rovnováhy, ktorá sa môže použiť na vyjadrenie odporu jedného rezistora, ak sú ostatné známe
![]() .
.
Kontrolné otázky:
1. Aké by bolo znenie 2. Kirchhoffovho zákona, ak by sme miesto elektrického napätia zdrojov použili elektromotorické napätie?
2.
Je jednotný smer obiehania slučiek (pri písaní
rovníc podľa 2. Kirchhoffovho zákona) dôležitý, alebo si môžeme zvoliť
v slučkách rôzne smery obiehania?
3.
Ako postupujeme pri voľbe počtu rovníc pri riešení
siete?