14.1.3 Väzbová energia jadra a jeho stabilita

Energia, potrebná na to, aby sme jadro rozložili na jednotlivé voľné nukleóny s nulovou kinetickou energiou sa nazýva väzbová energia jadra. Pri vytvorení jadier spojením nukleónov sa táto energia uvoľní. Na základe Einsteinovho vzťahu medzi energiou a hmotnosťou môžeme väzbovú energiu vyjadriť:

(14 .1.3.1)

Energia odpovedajúca hmotnosti 1 u je 931,5 MeV. (V príkladoch môžeme potom výhodne použiť namiesto c² ekvivalent: 931,5 MeV/u). Pre porovnanie: väzbová energia elektrónov v elektrónovom obale atómu je rádove v eV, zatiaľčo väzbové energie jadier sú v MeV.

Pri porovnávaní stability jadier je vhodné používať energiu pripadajúcu na jeden nukleón:

(14 .1.3.2)

V závislosti e(A) (obr.14.1.3.1) pozorujeme lokálne maximá v prípadoch, keď počet protónov

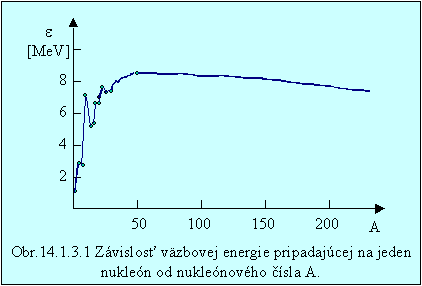
alebo neutrónov sa rovná magickým číslam 2, 8, 20, 28, 50, 82, 126, 152 a takéto jadrá vykazujú výnimočnú stabilitu. Maximum hodnoty e_max = 8,5 MeV sa pozoruje pre nukleónové číslo A = 50. V oblasti A Î(50, 150) ostáva e takmer konštantná, pre A > 150 hodnota e klesá. Z uvedeného vyplýva, že sily, ktoré viažu nukleóny do jadier sa nasycujú. Pokles krivky pri veľkých hodnotách A znamená, že nukleóny sú pevnejšie viazané v dvoch stredne hmotných nuklidoch ako v jednom nuklide s veľkým hmotnostným číslom. Teda energia sa môže uvoľniť pri jadrovom štiepení. Pokles krivky väzbovej energie e pre malé A zasa vypovedá o tom, že zlúčením dvoch nuklidov s malým hmotnostným číslom do stredne hmotného sa tiež uvoľní energia – ide o jadrovú syntézu, ktorá napr. prebieha vnútri Slnka a iných hviezd.

Hodnoty energie jadra sú podobne ako energie atómu kvantované. Jadro sa môže nachádzať len v istých diskrétnych energetických stavoch, pri prechode jadra z vyššej na nižšiu energetickú hladinu je emitovaný fotón v oblasti g - žiarenia elektromagnetického spektra.

––––––––––––––––––––––––––––––––––––––

Príklad 14.1.3.1 Vypočítajte koľko energie je treba na oddelenie všetkých nukleónov tvoriacich jadro izotopu zlata ¹⁹⁷Au, hmotnosť neutrálneho atómu Au vyjadrená v atómových hmotnostných jednotkách je m_a = 196,966543 u. Vypočítajte väzbovú energiu pripadajúcu na jeden nukleón v tomto nuklide!

Riešenie: Väzbovú energiu, teda energiu potrebnú na oddelenie všetkých nukleónov, vypočítame zo vzťahu:

kde hmotnosti atómu vodíka a neutrónu vyjadrené v atómových hmotnostných jednotkách sú:

m_H = 1,007825 u, m_n = 1,008665 u a pre nuklid Au je atómové číslo Z = 79, a počet neutrónov je:

N = A – Z = 197 – 79 = 118. Po dosadení dostaneme:

Väzbová energia na jeden nukleón je:

––––––––––––––––––––––––––––––––––––––