13.2.3 Atóm s viacerými elektrónmi

S výnimkou atómu vodíka, všetky atómy v  neionizovanom stave obsahujú viac ako

jeden elektrón. Bohrov model atómu bol schopný vysvetliť zákonitosti spektier atómu vodíka a vodíku podobných atómov. (Vodíku podobné atómy sú ionizované atómy len s jediným elektrónom na poslednej sfére, napr. Li²⁺).

V základnom stave jediný elektrón atómu vodíka je vo svojom najnižšom kvantovom stave, určenom štyrmi kvantovými číslami: hlavným kvantovým číslom n =1, orbitálnym (vedľajším) kvantovým l = 0, magnetickým kvantovým číslom m_l = 0, magnetickým spinovým kvantovým číslom m_s = ½. Stavy elektrónov v atóme sú určené štyrmi kvantovými číslami (n, l, m_l, m_s), ktorých označenie, dovolené hodnoty a význam udáva tabuľka 13.2.3.1 .

Tab. 13.2.3.1 Stavy elektrónov v atóme

Kvantové číslo	Označenie	Dovolené hodnoty	Význam
hlavné	n	1,2,3,....	vzdialenosť od jadra energiu stavu
orbitálne	l	0, 1,2,....., (n-1)	veľkosť orbitálneho momentu hybnosti L
magnetické	ml	0, ±1, ±2, .... ±l	veľkosť Lz (priemet L do osi z)
magnetické spinové	ms	±1/2	veľkosť Sz (priemet spinového momentu hybnosti S do osi z)

Čo je však základný stav atómu s viacerými elektrónmi, napr. u uránu s 92 elektrónmi? Je možné určiť koľko elektrónov môže mať daná množina kvantových čísiel (n, l, m_l, m_s)? Odpoveď na tieto otázky, na základe štúdia atómových spektier podal rakúsky teoretický fyzik Wolfgan Pauli (1900- 1958). Vychádzal zo skutočností, že v spektrách rôznych prvkov, okrem vodíka, chýba vždy rad čiar, ktoré odpovedajú prechodom medzi stavmi s istými kombináciami kvantových čísiel. Táto skutočnosť bola sformulovaná Nielsom Bohrom v tzv. výberovom pravidle:

Dovolený je len taký preskok elektrónu z dráhy jednej sféry (orbity) do dráhy inej sféry, pri ktorom:

· sa hlavné kvantové číslo môže meniť o ľubovolný počet jednotiek, nemôže však ostať nezmenené;

· vedľajšie kvantové číslo l sa zmení o jednotku, t.j. D l = ±1;

· magnetické kvantové číslo ostane nezmenené, alebo sa zmení o jednotku, t.j. D m _l = 0, ±1.

Wolfgan Pauli ukázal, že každá chýbajúca spektrálna čiara a im zodpovedajúci chýbajúci atómový stav, predstavuje dva alebo viacej elektrónov s  rovnakými kvantovými číslami. Konštatovanie tohto empirického poznania sformuloval do vylučovacieho princípu, dnes známeho pod názvom

Pauliho vylučovací princíp:

Žiadne dva elektróny v atóme sa nemôžu nachádzať v rovnakom kvantovom stave. Každý elektrón v atóme musí mať rôzny súbor štyroch kvantových čísiel n, l, m_l a m_s.

Pauliho princíp celkom presne určuje hranicu pre počet elektrónov v danej sfére, resp. podsfére. Podsféra je charakterizovaná určitým hlavným kvantovým číslom a orbitálnym kvantovým číslom l. Pre každé l existuje 2l+1 rôznych hodnôt magnetického kvantového čísla m_l a dve možné hodnoty spinového kvantového čísla m_s. Každá podsféra môže obsahovať najviac 2(2l+1) elektrónov a každá sféra s daným n môže teda obsahovať maximálny počet elektrónov 2n², pretože

(13.2.3.1)

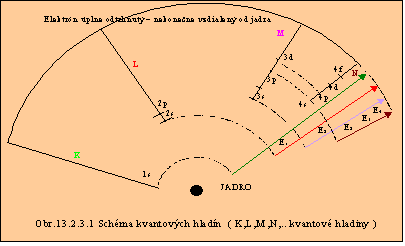
Atómová sféra alebo podsféra, ktorá je obsadená maximálnym počtom elektrónov, sa nazýva uzavretá sféra, resp. podsféra. Obsadzovanie elektrónov v atóme pre n = 1 až 4 podáva tabuľka 13.2.3.2, z ktorej aj vyplýva usporiadanie prvkov v Mendelejevovej periodickej sústave prvkov. Možné prechody medzi jednotlivými sférami sú znázornené na obr. 13.2.3.1

Tab. 13.2.3.2 Obsadzovanie elektrónov v  atóme s viacerými elektrónmi s hlavným kvantovým číslom n = 1- 4.

n	Označenie sféry	ℓ	názov podsféry l	Označenie dráh elektrónov	ml	Počet dráh	ms	počet elektrónov
								v podsfére	celkový vo sfére
1	K	0	s	1s	0	1	±1/2	2	2.1^2= 2
2	L	0 1	s p	2s 2p	0 -1,0,+1	1 3	±1/2 ±1/2	2 6	2.2^2= 8
3	M	0 1 2	s p d	3s 3p 3d	0 -1,0,+1 -2,1,0,+1,+2	1 3 5	±1/2 ±1/2 ±1/2	2 6 10	2.3^2= 18
4	N	0 1 2 3	s p d f	4s 4p 4d 4f	0 -1,0,+1 -2,-1,0,+1,+2 -3,-2,-1,0+1,+2,+3	1 3 5 7	±1/2 ±1/2 ±1/2 ±1/2	2 6 10 14	2.4^2= 32

Všimnime si, že usporiadanie do jednotlivých riadkov v tabuľke 13.2.3.2 odpovedá skutočnosti zapĺňania orbít s hlavným kvantovými číslami 1 až 4. V prírode sa pozorovalo zaplnenie až po n =7, ktoré odpovedá  Mendelejevovej periodickej tabuľky.

Druhým základným pravidlom, ktorým sa riadi elektrónová štruktúra s mnohými elektrónmi, je:

· Systém častíc je stabilný, ak jeho celková energia je minimálna .

Dôsledkom tohto pravidla je i skutočnosť, že kedykoľvek je to len možné, elektróny v atóme vo všeobecnosti ostávajú nespárené, t.j. majú rovnobežné spiny. Tento princíp sa nazýva Hundove pravidlo.

Poznámka: K vysvetleniu ostatných skutočností v mnohoelektrónových atómoch, je nevyhnutné sa oboznámiť napr. s celkovým momentom hybnosti J, definovaným ako vektorový súčet hybností jednotlivých elektrónov, a to momentov ako orbitálnych tak i spinových. Keďže počet elektrónov (ako i počet protónov) v neutrálnom atóme určuje protónové číslo Z, celkový moment hybnosti J

J = (L₁+ L₂+ L₃+....+ L_Z) + ( S₁+ S₂ +S₃ +.... +S_Z ).

Sú možné dva spôsoby skladania orbitálnych a spinových momentov v mnohoelektrónových atómoch. S týmito podrobnosťami sa čitateľ môže oboznámiť bližšie v monografiách kvantovej fyziky.

Kontrolné otázky :

1. Akým súborom čísiel je určený kvantový stav elektrónu v atóme ?

2. Ktoré kvantové číslo určuje orbitu, na ktorej sa pohybuje elektrón?

3. Kedy hovoríme, že sa elektrón nachádza v základnom stave?

4. Vyslovte Bohrov vylučovací princíp.

5. Môžeme pozorovať preskoky elektrónov medzi jednotlivými podsférami danej sféry?

6. Aký význam má magnetické kvantové číslo m _l ?

7. Aký význam má hlavné kvantové číslo n?

8. Aký význam má orbitálne kvantové číslo l?

9. Vyslovte Pauliho vylučovací princíp.

10. Na akom princípe možno vysvetliť usporiadanie atómov do periodickej sústavy prvkov?

11. Vysvetlite prečo v prvej perióde Mendelejevovej tabuľky sa nenachádzajú na voľných miestach iné prvky.

12. Akému kvantovému číslu prináleží druhý riadok v periodickej sústave prvkov?

13. Na základe akého pravidla sa vysvetľuje feromagnetizmus železa? (Súvisí s orientáciou spinov).