11.2.3 Súhrn rovníc elektromagnetického poľa

V kapitole 8. o elektrostatike bola odvodená prvá Maxwellova rovnica :

div D = r_v

(11.2.3.1)

v ktorej D je vektor elektrickej indukcie a r_v objemová hustota voľného elektrického náboja. Treba ešte raz zdôrazniť, že ide o voľný elektrický náboj, teda náboj, ktorý sa môže premiestňovať na makroskopické vzdialenosti. K veľkosti vektora D neprispievajú viazané náboje, napríklad náboje spolarizovaného dielektrika. Prvá Maxwellova rovnica je zovšeobecnením Coulombovho zákona i Gaussovej vety.

V kapitole 10. o magnetostatike bola odvodená druhá Maxwellova rovnica :

div B = 0

(11.2.3.2)

ktorá vyjadruje skutočnosť, že statické magnetické pole nemá podobné (bodové) zdroje ako elektrostatické pole, že magnetické indukčné čiary nemajú začiatok a koniec, ale že sú to uzavreté krivky.

Prvá a druhá Maxwellova rovnica sa týkajú stacionárnych polí - elektrostatického a magnetostatického, ktoré sa s časom nemenia. Tretia a štvrtá Maxwellova rovnica opisujú nestacionárne polia a vyjadrujú významnú prírodnú zákonitosť - zmena magnetického poľa vedie ku vzniku elektrického poľa a naopak, časovo premenné elektrické pole má za následok vznik magnetického poľa.

V paragrafe 11.2.1 bola odvodená tretia Maxwellova rovnica :

rot E = -(¶B/ ¶t) ,

(11.2.3.3)

v ktorej E je vektor intenzity elektrického poľa a B je vektor magnetickej indukcie. Rovnica vyjadruje vznik elektrického poľa v časovo premenlivom magnetickom poli.

V paragrafe 11.2.2 bola odvodená štvrtá Maxwellova rovnica :

rot H = j + (¶D/ ¶t) ,

(11.2.3.4)

v ktorej H je vektor intenzity magnetického poľa, D vektor elektrickej indukcie a j vektor prúdovej hustoty, reprezentujúci transport voľného elektrického náboja (nie viazaného, t.j. nevzťahuje sa na mikroskopické prúdy cirkulujúce v molekulách). Rovnica vyjadruje skutočnosť, že magnetické pole vzniká v okolí vodičov elektrického prúdu, i v časovo premenlivom elektrickom poli. V podstate obsahuje aj rovnicu kontinuity elektrického prúdu, ak si uvedomíme súčasnú platnosť prvej Maxwellovej rovnice.

V uvedených štyroch Maxwellových rovniciach vystupujú derivácie (priestorové i časové) štyroch základných vektorov E, D, B, H, opisujúcich elektromagnetické pole. Preto sa niekedy uvádzajú pod názvom Maxwellove rovnice v diferenciálnom tvare. Každá z týchto rovníc má svoj ekvivalent v integrálnom tvare. V nasledujúcich riadkoch sú tieto ekvivalenty uvedené po súvisiacich dvojiciach :

(11.2.3.5)

K poslednej zo série rovníc v integrálnom tvare treba uviesť, že do súčtu makroskopických prúdov I_k treba zarátať aj Maxwellove posuvné prúdy. Odvodenie vzťahov medzi integrálnym a diferenciálnym tvarom Maxwellových rovníc možno nájsť v príslušných paragrafoch.

Na úplný opis javov v elektromagnetickom poli, najmä v látkovom prostredí, nevystačíme s Maxwellovými rovnicami. V dielektriku treba na opis jeho spolarizovaného stavu pridať vektor elektrickej polarizácie P a v magnetiku vektor magnetickej polarizácie J , resp. vektor magnetizácie M . Tieto vektory vstupujú do tzv. materiálových vzťahov :

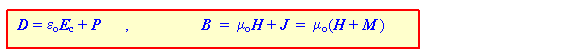
(11.2.3.6)

kde D je vektor elektrickej indukcie, E_c vektor výslednej intenzity elektrického poľa v dielektriku (súčet intenzít vytvorených voľnými i viazanými nábojmi), B vektor magnetickej indukcie (vyvolaný makro- i mikroprúdmi) e_o elektrická konštanta (permitivita vákua) a m_o

magnetická konštanta (permeabilita vákua).

Na opis prúdov treba pridať rovnicu kontinuity

(11.2.3.7)

v ktorej j je vektor prúdovej hustoty a r objemová hustota voľného elektrického náboja. Z rovnice kontinuity v stacionárnom stave vyplýva prvý Kirchhoffov zákon. Vzťah medzi prúdovou hustotou j a pôsobiacim elektrickým poľom s intezitou E vyjadruje Ohmov zákon v diferenciálnom tvare

(11.2.3.8)

kde g je konduktivita prostredia (prevrátená hodnota rezistivity). Integráciou Ohmovho zákona v diferenciálnom tvare možno získať Ohmov zákon pre úsek vodiča, ako aj druhý Kirchhoffov zákon pre elektrický obvod.

Elektromagnetické pole charakterizujeme aj objemovou hustotou energie. V paragrafoch 8.x.x a 11.1.5 boli odvodené vzťahy pre objemové hustoty energie v elektrickom, resp. v magnetickom poli. Sčítaním týchto parciálnych vzťahov dostaneme súhrnný vzorec pre objemovú hustotu energie elektromagnetického poľa :

(11.2.3.9)

V tomto vzorci vystupujú teda všetky štyri základné vektory opisujúce elektromagnetické pole.

Kontrolné otázky

1. Napíšte všetky štyri Maxwellove rovnice v diferenciálnom tvare.

2. Ktoré z Maxwellových rovníc sa týkajú stacionárneho stavu ?

3. Aký vzájomný vzťah medzi elektrickým a magnetickým poľom vyplýva z tretej a štvrtej Maxwellovej rovnice ?

4. Napíšte Maxwellove rovnice v integrálnom tvare

5. Čo vyjadrujú materiálové vzťahy ?

6. Uplatnia sa materiálové vzťahy vo vákuu ?

7. Ktorými základnými rovnicami opisujeme deje súvisiace s vedením elektrického prúdu ?

8. Napíšte a vysvetlite rovnicu kontinuity pre elektrický prúd.

9. Uveďte rozdiel medzi vektorom magnetickej polarizácie a vektorom magnetizácie.

10. Aké významné vzťahy (zákony) možno odvodiť z Ohmovho zákona v diferenciálnom tvare ?

11. Aký zákon pre elektrický prúd vyplýva z rovnice kontinuity v stacionárnom stave ?