2.1.6 Derivácia vektora, ktorého veľkosť sa nemení

Pri pohybe častice po kružnici, ak jej polohový vektor r vzťahujeme na stred kružnice, tento sa otáča uhlovou rýchlosťou w, ale nemení svoju veľkosť. Nech r = Rr , kde r je jednotkový vektor a R polomer kružnice. Podobne nech w = w w_o , kde w_o je jednotkový vektor rovnobežný s vektorom w a w jeho veľkosť . Deriváciou polohového vektora podľa času dostaneme rýchlosť častice : v = dr / dt . Pri pohybe po kružnici platí skalárny vzťah

v = Rw (2.1.5.4), ktorý vyjadruje veľkosť vektora obvodovej rýchlosti. Pritom vieme, že vektor v je rovnobežný s dotyčnicou kružnice, poznáme teda aj jeho smer určený jednotkovým vektorom t : v = v t .

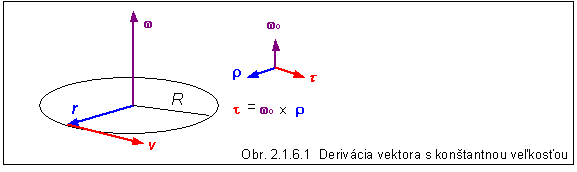
Preto môžeme napísať vzťah v = (R w) t . Pomocou obrázku si možno overiť, že jednotkový vektor t možno vyjadriť ako vektorový súčin t = w_o ´ r . Tak dostaneme vzťah

dr / dt = v = (R w) t = (R w) (w_o ´ r ) = (w w_o ´ R r ) = w ´ r , t.j.

(dr / dt) = w ´ r , (2.1.6.1)

ktorý vyjadruje deriváciu vektora s nemeniacou sa veľkosťou.

Derivácia vektora, ktorý sa s časom nemení (t.j. nemení sa jeho veľkosť, ani smer), sa rovná nule. Ak sa vektor s časom mení tak, že sa nemení jeho veľkosť, potom sa musí otáčať istou uhlovou rýchlosťou. Táto vstupuje do vzorca (2.1.6.1), vyjadrujúceho jeho deriváciu.

Vzťah (2.1.6.1) sa týka derivácie ľubovoľného vektora s nemeniacou sa veľkosťou, napríklad jednotkového vektora, ktorý sa otáča. Preto pre jednotkový vektor r , otáčajúci sa uhlovou rýchlosťou w platí :

dr / dt = w ´ r . (2.1.6.2)

Kontrolné otázky

1. Kedy je derivácia vektora rýchlosti nulová?

2. Napíšte vzťah vyjadrujúci súvislosť obvodovej a uhlovej rýchlosti hmotného bodu pohybujúceho sa po kružnici.

3. Napíšte vzťah určujúci deriváciu vektora q podľa času , ak jeho veľkosť je konštantná.