Study of Mixed Cation
Effect in Ion Conductivity Glasses Using Electrical Conductivity Spectra
P. Hockicko a,
P. Bury a, M. Jamnický b
and I. Jamnický a
a Department of Physics, University of Žilina, 010 26
Žilina, Slovakia
b Department of Ceramic, Glass and Cement, Slovak
Technical University, 812 37 Bratislava, Slovakia
email: hockicko@fel.utc.sk
Abstract
The acoustical and electrical methods have been already proved to be an
effective tool for studying the fundamental structural, mechanical and also
transport of the ionic materials. Thus we can determine the relationship
between mechanical and electrical properties of the new kinds of ion conductive
glasses. In the contribution we present both the data obtained by electrical
measurement (d.c. and a.c. conductivity) and acoustical measurement (acoustical
attenuation) of ion conductive glasses of the system CuI-CuBr-Cu2O-P2O5
for different glass composition and outline the possible relation between its
acoustical and electrical properties. The expected mixed cation effect in the
electrical conductivity and acoustical attenuation spectra of several systems
of CuI-CuBr-Cu2O-P2O5 that differ by the
concentration of its components ion conductivity glasses is identified and
their interrelation is analyzed. We observe characteristic effects in frequency
response of the complex electrical conductivity and in the magnitudes of
acoustic attenuation.
introduction There is a considerable interest in the experimental
study of glassy materials with the fast ion transport, particularly in their
ion transport mechanisms, because they can play an important role in a number
of modern electrochemical devices, such as solid-state batteries,
electrochronic displays, and sensors [1,2]. The ion conductive glasses have
several advantages comparing with crystalline materials because of their easy
preparation, their stability composition ranges, the absence of grain
boundaries, the isotropic properties and the large available composition
variability.
Ion conductive glasses have common structural characteristic, that includes a highly ordered, immobile framework complemented by a highly disordered interstitial sublattice in which carriers are randomly distributed and in which the number of equivalent sites is greater than the number of available ions to fill them. These low potential sites comprising the carrier sublattice must be sufficiently interlined to provide continuous transport paths necessary for optimal movement of ions [3].
The investigation of conductivity spectra of
ionic glasses reflects the basic features of the relaxation and transport
mechanisms of the mobile ions [4]. The high ion conductivity at room
temperature is the most important criterion, which should be met by the fast
ion conductive glasses [5,6]. However, the transport mechanisms can be
investigated also by acoustic methods, that can have some advantages comparing
to electrical ones as the high sensitivity, absence of contact phenomena and so
on [6,7].
The glasses, which contain Cu+
conductive ions, have similar electronic configuration and smaller ionic radii
in comparison with Ag+ ion conducting glasses in various
glass-forming systems. The conductivity of glasses is affected not only by the
type of conductive ions, but also strongly depends on „glass forming“ oxide,
but Cu+ ion conducting glasses are only known in very limited
glass-forming systems. Phosphate glasses containing Cu+ conducting
ions are good ionic and the highest conductivity has been recorded in systems
containing large fractions of cuprous halides, such as CuI or CuBr [8,9].
Moreover, if two different kinds of halide anions are mixed into cation
conducting glasses [9], a positive deviation of the electrical conductivity
from the additivity rule can be observed (mixed anion effect).
In this contribution we present some electrical
and acoustical properties of glasses prepared in the systems CuI-CuBr-Cu2O-P2O5. The main purpose of the contribution is to
investigate ion transport mechanisms and to determine the relation between
acoustical and electrical properties considering the various glass
compositions.
 EXPERIMENTAL PROCEDURE The procedure of glasses preparation in the system CuI-CuBr-Cu2O-P2O5 from commercial reagents (Fluka)
represented the procedure already described [10]. The compositions of glass
samples are summarized in Table 1.
The samples for acoustical attenuation and electrical conductivity
measurementswere cylindrical in shape (area » 1 cm2, thickness » 1.6 - 2.0 mm). Gold electrodes were
sputtered onto the sample surfaces for electrical investigation. The frequency
and temperature dependencies of electrical conductivity (d.c. and a.c. in the
frequency range from 50 Hz up to 1 MHz) were measured using FLUKE PM 6306
impedance analyser and in the temperature range of 140-365 K. The measured
complex impedance allowed us to obtain the bulk d.c. and a.c. conductivity of
glass samples by means of the usual impedance analysis.
EXPERIMENTAL PROCEDURE The procedure of glasses preparation in the system CuI-CuBr-Cu2O-P2O5 from commercial reagents (Fluka)
represented the procedure already described [10]. The compositions of glass
samples are summarized in Table 1.
The samples for acoustical attenuation and electrical conductivity
measurementswere cylindrical in shape (area » 1 cm2, thickness » 1.6 - 2.0 mm). Gold electrodes were
sputtered onto the sample surfaces for electrical investigation. The frequency
and temperature dependencies of electrical conductivity (d.c. and a.c. in the
frequency range from 50 Hz up to 1 MHz) were measured using FLUKE PM 6306
impedance analyser and in the temperature range of 140-365 K. The measured
complex impedance allowed us to obtain the bulk d.c. and a.c. conductivity of
glass samples by means of the usual impedance analysis.
The acoustical attenuation was
measured using MATEC attenuation comparator for longitudinal acoustic wave of
frequency 18 MHz generated by quartz transducer. The quartz buffer was used to
separate the signal from quite short sample.
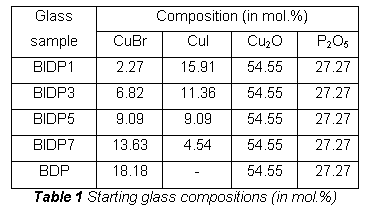
 RESULS The
representative result of d.c. conductivity measurement (sample BIDP7) as a function
of temperature is illustrated in Fig. 1. Four different slopes (denoted 1 - 4)
of measured can be recognized. However, very interesting feature, not observed
before [7], is jump in the curve indicated as slope (3). All of the temperature dependencies of d.c. glass conductivity can be
fitted by the equation:
RESULS The
representative result of d.c. conductivity measurement (sample BIDP7) as a function
of temperature is illustrated in Fig. 1. Four different slopes (denoted 1 - 4)
of measured can be recognized. However, very interesting feature, not observed
before [7], is jump in the curve indicated as slope (3). All of the temperature dependencies of d.c. glass conductivity can be
fitted by the equation:
|
|
s = s0 exp (-Ea / kBT) , |
(1) |
where Ea
is the activation energy, kB
is the Boltzman constant and T
is the thermodynamic temperature. The pre-exponential factor s0 is a function of temperature, too. Because of
that the factor sT is used in Arrhenius plots of d.c. conductivity. The plots of the
temperature dependencies of d.c. conductivity indicate more then two transport
mechanisms with activation energies Ea1, Ea2,
maybe Ea3 and Ea4 from higher to lower
temperatures. Activation energies calculated from Arhenius plots of d.c.
conductivity are summarized in Table 2 for all glass samples.
![Textové pole: Glass sample Ea1 [eV] Ea2 [eV] Ea4 [eV]
BIDP1 0,47 0,54 0,36
BIDP3 0,46 0,58 0,42
BIDP5 0,44 0,54 0,42
BIDP7 0,43 0,49 0,41
BDP 0,40 0,51 0,38
Table 2 Summary of activation energies calculated from Arrhenius plots of d.c. conductivity](./apcom_03_soubory/image004.gif) All of the prepared glasses have
high ionic conductivity at room temperature (10-2 - 10-4W-1m-1). The samples containing the
same molar amount of glass-forming components exhibit very close values of
activation energies Ea4 characterising the transport
mechanisms at lower temperatures. However, the activation energy Ea1
that characterises the ion transport at higher temperatures depends on the
ratio of CuI to CuBr responsible for Cu+ ion concentrations and
indicates similar role of both components in the process of Cu+
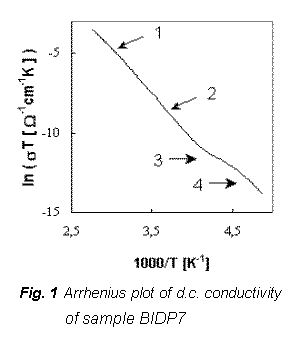
mobile ion that govern the conductivity. A.c. conductivity measured at various
temperatures is illustrated in Fig. 2 for glass sample BIDP1.
All of the prepared glasses have
high ionic conductivity at room temperature (10-2 - 10-4W-1m-1). The samples containing the
same molar amount of glass-forming components exhibit very close values of
activation energies Ea4 characterising the transport
mechanisms at lower temperatures. However, the activation energy Ea1
that characterises the ion transport at higher temperatures depends on the
ratio of CuI to CuBr responsible for Cu+ ion concentrations and
indicates similar role of both components in the process of Cu+
mobile ion that govern the conductivity. A.c. conductivity measured at various
temperatures is illustrated in Fig. 2 for glass sample BIDP1.
The
obtained a.c. conductivity measurements correspond to the complete conductivity
spectra obtained from glassy samples [5,10]. However, because of the limited
frequency range, only two regimes (II and III) of [5,10] which are due to
hopping motion are differed by breaks on individual curves could be recognized.
The transport hopping process can be explained by slightly modified jump
relaxation model [5]. Similarly as d.c. measurements a.c. spectra show jump,
that can be recognized at lover frequencies and higher temperatures.
The
measurements of temperature dependence of acoustic attenuation (Fig. 3)
indicate one broad attenuation maximum in all investigated samples, in which we
can distinguish two or three separated peaks with a different position for
every sample. The another peak can be seen at lover temperature range.
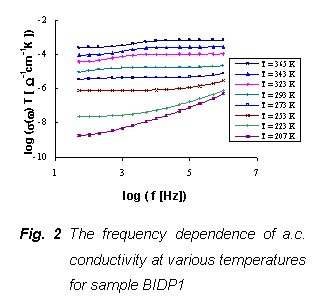
The peaks at the broad maxima of acoustical attenuation
spectra indicate transport mechanisms with activation energies very close to
that determined in d.c. electric measurements. The study of acoustical
attenuation results in an Arrhenius – type relation between peak temperature
and applied frequency [10]:
|
|
n = n0 exp (-Ea / kBTpeak)
, |
(2) |
![Textové pole: Glass sample [eV] [eV] [eV]
BIDP1 0,47 0,41 0,21
BIDP3 0,46 0,41 0,26
BIDP5 0,48 0,40 0,27
BIDP7 0,46 0,39 0,26
Table 3 Summary of activation energies calculated from Tpeak of acoustic attenuation](./apcom_03_soubory/image012.gif) where the values for preexponential factor n0 are of order of 1014 Hz, but they
are again depended on temperature. The activation energies calculated from the
peak temperatures Tpeak are summarized in Table 3 for four
glass samples.
where the values for preexponential factor n0 are of order of 1014 Hz, but they
are again depended on temperature. The activation energies calculated from the
peak temperatures Tpeak are summarized in Table 3 for four
glass samples.
CONCLUSION We have studied the mixed cation
effect using the conductivity spectra and in the acoustical attenuation spectra
of ion conductive glasses in the system CuI-CuBr-Cu2O-P2O5.
The experimental investigation of acoustical and electrical properties of ion
conductive glasses showed the important influence of chemical composition and
ion transport mechanisms and indicated also more than two transport mechanisms.
The fact that the activation energies determined from both electrical
conductivity measurements and acoustical attenuation spectra have very similar
values proved that the same mechanisms can influence both electrical and
acoustical losses in ion conductive glasses.
ACKNOWLEDGEMENT The authors would like to thank Mr. F. Černobila for technical assistance. This work was partly financially supported by Grant 1/914/02 of the Ministry of Education of the Slovak Republic.
References
[1]
M. D. Ingram, Phil. Mag. 60 (1998) 729.
[2]
S. W. Martin, J. Amer. Ceram. Soc. 74 (1991) 1767.
[3] D. P. Button, L. S.
Mason, H. L. Tuller and D. R. Uhlmann, Solid State Ionics 9/10 (1983)
585.
[4] N. Machida, M.
Chusho, T. Minami, J. Non-Cryst. Solids 101 (1988) 70.
[5]
K. Funke, Sol. State Ionics 94 (1997) 27.
[6] E. V. Charnaya, B. F. Borisov, A. A. Kuleshov, Proc. World Congress on Ultrasonics, Berlin 1995, p. 483.
[7] P. Bury, P. Hockicko, M. Jamnický and I. Jamnický, Proc. of the 32nd International Acoustical Conference - (EAA) Symposium, Banská Štiavnica 2002, p. 67.
[8]
P. Znášik and M. Jamnický, Solid St. Ionics 95 (1997) 207.
[9]
Ch. Lin and C. A. Angel, Solid St. Ionics 13 (1984) 105.
[10]
K. Funke, B. Roling, M. Lange, Sol. State Ionics 105 (1998) 195.
[11]
B. Roling, A. Happe, M. D. Ingram and K.
Funke, J. Phys. Chem. B 103 (1999)
4122.