1. Introduction
It is known that the investigation of acoustic spectra of ionic glasses can reflect the basic features of the relaxation and transport mechanisms of the mobile ions. The acoustic attenuation measurement seems to be a useful technique for nondestructive investigation of transport mechanisms in conductive glasses and compared to the electrical ones they have even some advantages as high sensitivity, the absence of contact phenomena and so on [1,2]. Acoustical measurements made over a wide range of frequencies and temperatures can characterize different relaxation processes according to corresponding transport mechanisms due to a strong acousto-ionic interaction.
The ion transport properties of many ion conducting glasses, melts and crystals are similar [3]. Ion conductive glasses have common structural characteristic that includes a highly ordered, immobile framework complemented by a highly disordered interstitial sublattice in which carriers are randomly distributed and in which the number of equivalent sites is greater than the number of available ions to fill them. These low potential sites that comprise the carrier sublattice must be sufficiently interlined to provide continuous transport paths necessary for optimal movement of ions [4]. In glassy electrolytes, the mobile ions encounter different kinds of site and ionic hopping motion and relaxation processes connected with charge mobility so that modified jump relaxation model can be used for transport mechanisms description [5].
The conductivity of glasses is affected not only by the type of conductive ions, but also strongly depends on „glass forming“ oxide. Phosphate glasses containing Cu+ conductive ions are good ionic conductors with room temperature conductivity of the order 10-3 W-1cm-1. The highest conductivity has been recorded in systems containing large fractions of cuprous halides, such as CuI or CuBr [6].
In this contribution we present theoretical description of experimental results obtained by acoustic investigation of the set of glasses prepared in the system CuI-CuBr-Cu2O-P2O5 with the purpose to study ion transport mechanisms in these ion conductive glasses and to find the role of cuprous halides producing Cu+ ions.
2. Theoretical models
The formal theory of all relaxation processes is similar. A comparison between the electric and acoustic response functions may give useful insights into the dynamic behaviour of ion conducting glasses. In practice, the electrical data are obtained in the frequency domain, while the experimental data of acoustic attenuation are usually available in a narrow frequency region and over a wide temperature range. It is well known that the frequency dependent conductivity of ionic glasses is extremely informative and that there have not been systematic comparative studies of mechanical and electrical processes in the same glasses. Moreover, in many electrical investigations, the data have not been analyzed as a function of ion content in a given glass-forming system [7].
In dilute system containing a low concentration of mobile ions the attenuation may be described as a Debye-like, single relaxation time processes in which the individual ion hops occur independently of each other. In such cases, the attenuation a for a wave of angular frequency w takes the form [8]
|
|
|
(1) |
where the parameter D is relaxation strength and it determines the magnitude of the attenuation peak. It is related to the strain dependence of the mobile ion site energy, or deformation potential B by
|
|
|
(2) |
in which N is the number of mobile ions, v is the velocity of the sound wave, r is the density of the solid, T is absolute temperature and kB is the Boltzmann constant.
The term in equation (1) in the round brackets describes a Debye peak. The acoustic attenuation will exhibit a maximum when the relaxation time tis comparable to the period (1/w) of the acoustic perturbation and the condition wt is equal to 1, where [9]
|
|
|
(3) |
is the most probable relaxation time. The relaxation processes, described by an Arrhenius equation (3), are characterized by activation energy EA for jumps over the barrier between two potential minima and typical relaxation frequency of ion hopping 1/t0» 1013 – 1014 s-1.
In fact all the investigated relaxation peaks are much broader than Debye peak. It can be interpreted as arising from the existence of a distribution of relaxation times due to random deviations in the local arrangement of the system. According to this hypothesis that the relaxation losses are not to large one can write for the acoustic attenuation, in case of a distribution f(t) of relaxation times [9]
|
|
|
(4) |
As a consequence, the t distribution can be connected with a distribution of activation energies E, representing the heights of the barriers that the ions must surmount to go into the near allowed positions. A useful form of equation (4) that takes into account only E distribution can be derived by the microscopic theory of Jäckle et al. [9]
|
|
|
(5) |
where an average deformation potential B expresses the coupling between the ultrasonic stress and the system and P(E) represents the E distribution function. We can assume for P(E) a Gaussian distribution [10]
|
|
|
(6) |
in which N is the total number of jumping particles per unit volume, Em the most probable activation energy and E0 the width of the distribution.
This approach depends on the assumption that ion migration may be treated in terms of a set of non-interacting Debye-like processes. However, in solid electrolytes the mobile ion concentrations are large and conduction mechanisms are thought to be cooperative. The relaxation phenomena observed in a wide variety of materials exhibit a power-law type of frequency dependence. The relationship to Debye behaviour is expressed in the form [8]
|
|
|
(7) |
where m and n are power-law exponents, which take values between 0 and 1. When m = 1 and n = 0, equation (7) reduces to the equation for a single Debye-like process.
Two functions have mainly been used to fit mechanical loss data [11]. The first function is the Kohlrausch-Williams-Watts (KWW) function
|
|
|
(8) |
with 0 < b£ 1. The acoustical attenuation is then given by
|
|
|
(9) |
The second function is the double power law
|
|
|
(10) |
Using these functions, we can fit also the acoustic attenuation spectrum of the cuprous halides glasses.
3. Experimental details and results
The procedure of glasses preparation in the system CuI-CuBr-Cu2O-P2O5 from commercial reagents has been already described [12]. The set of systems of glasses was originally prepared to investigate the role of cuprous halides producing Cu+ ion keeping their ratio to the glass forming system constant [13]. Batches of 15 g were melted under a dry argon atmosphere to avoid the oxidation of Cu+ during melting and mixed in appropriate portion in silica ampoule at 933 K for 90 min. The glass melts were rapidly quenched by pressing them between two brass plates to a final thickness of » 2 mm. The resulting discs of 20 mm in diameter were kept between the plates until their temperature decreased to room temperature. Losses in weight during melting were < 1 %. To check the reproducibility of the results, all glasses were prepared three times.
The samples for acoustical attenuation measurements were cylindrical in shape (area » 1 cm2, thickness 1.6 - 2.0 mm). The composition of the complex set of glass samples was summarized in [13], presented samples are summarised in Tab. 1.
Tab. 1. Starting glass compositions (in mol.%)
|
Glass sample |
Composition (in mol.%) |
|||
|
CuBr |
CuI |
Cu2O |
P2O5 |
|
|
BIDP1 |
2.27 |
15.91 |
54.55 |
27.27 |
|
BIDP3 |
6.82 |
11.36 |
54.55 |
27.27 |
|
BIDP5 |
9.09 |
9.09 |
54.55 |
27.27 |
|
BIDP7 |
13.63 |
4.55 |
54.55 |
27.27 |
The acoustical attenuation was measured using MATEC attenuation comparator for longitudinal acoustic wave of frequency 13, 18 and 27 MHz generated by quartz transducer in temperature range of 140-380 K. The quartz buffer was used to separate the signal from quite short sample (Fig. 1).
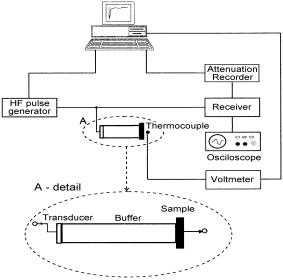
Fig. 1. Experimental arrangement foracoustic attenuation measurement
Acoustic attenuation peaks associated with ion hopping have been observed in glasses of different composition. The measurements of the temperature dependence of acoustic attenuation at the frequency n= 18 MHz indicate in all investigated samples one broad attenuation maxima at higher temperature, in which we can distinguish at least two separated peaks (Fig. 2). The acoustic attenuation is plotted as a function of temperature at a constant frequency. Using measurements at different frequencies, we can determine the activation energy of the loss peak EA from the equation [11]
|
|
|
(11) |
The temperature dependence of acoustic attenuation above 220 K has been analyzed using both conductivity and acoustic spectra [13] assuming the existence of two thermally activated relaxation processes of ions in connection with different kinds of sites. Low temperature peaks are usually related to the faster ion transport and high temperature peaks are related to slower mobile ions.
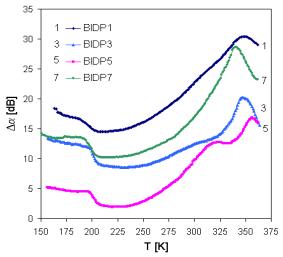
Fig. 2. Temperature dependence of acoustic attenuationof ion conductive glasses of the system CuI-CuBr-Cu2O-P2O5 for different glass composition. The individual spectra are shifted for the better resolution.
4. Results analyses
Using the theoretical models we can fit the temperature-dependent acoustic attenuation spectra at constant frequency. Usually, there is supposed [10], that the double power law (DPL) provides a slightly better fit than the KWW function or Debye-like process.
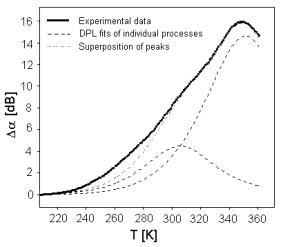
Fig. 3. Acoustics spectrum of sample BIDP1 (full line). Dashed lines represent the best fit of two relaxation processes.
We have, therefore, tried to use at first the DPL to fit the acoustic attenuation spectra of the investigated glasses (Fig. 3).
To fit the acoustic spectrum using the DPL model (Eq. (10)) was applied and the calculated lines gave an excellent agreement with measured spectrum in intermediate and high temperature range represented by spotted line in Fig. 3 illustrating the acoustic spectrum.
We can see, that the complete spectrum another sample illustrated in Fig. 4, cannot be fitted similarly as in the case of supposing only two relaxation processes. The additional third relaxation process should be taken into account with maximum at the temperature around 270 K.
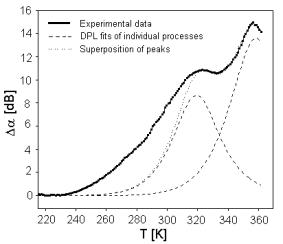
Fig. 4. Acoustics attenuation spectrum of sample BIDP5 (full line) and its theoretical supposing fit (spotted line) is superposition of two supposed relaxation processes (dashed lines).
The values of Tpeak can be easily and directly found from the theoretical fits. In this temperature region, the relaxation processes can be described by Arrhenius temperature dependencies of the relaxation time (Eq. (3)) and the values of EA can be determined using this function in first approximation. The preexponential factor t0 can be estimated from some typical frequencies characterized the shortest possible time processes of the relaxation [10] or determined from acoustic spectra obtained at various frequencies [12].
4. Conclusion
The experimental and theoretical investigation of ion conductive glasses in system CuI-CuBr-Cu2O-P2O5 proved that acoustical spectroscopy can be very useful technique for study of transport processes in fast ion conductive glasses.
An important finding from the present study is that the superposition attenuation peaks described by theoretical models can fit all acoustic attenuation spectra. It was found that the investigated relaxation process could be described by a relaxation theory. Using the theoretical models we can describe the relaxation processes and find some ion parameters.
The acoustic attenuation spectra of all investigated ion conducting glasses prepared in the system CuI-CuBr-Cu2O-P2O5 consist of more then two thermally activated relaxation processes for temperatures over 220 K. The superposition of three loss peaks with different activation energies can better fit the investigated spectrum of the glasses.
Further analyses of acoustic spectra obtained by investigation of glass samples with different compositions in wider temperature and frequency range should be done for better understanding of ion transport mechanisms for various types of the investigated ion conducting glasses.
Acknowledgement
The authors would like to thank Mr. F. Černobila for technical assistance. This work was partly financially supported by Grant 1/9141/ 02 of the Ministry of Education of the Slovak Republic.
References
[1] E. V. Charnaza, B. F. Borisov, A. A. Kuleshov: Proc. World Congress on Ultrasonics, Berlin (1995) 483.
[2] B. Roling, A. Happe, M. D. Ingram and K. Funke:J. Phys. Chem. B 103 (1999) 4122.
[3] K. Funke, B. Roling, M. Lange: Sol. State Ionics 105 (1998) 195.
[4] D. P. Button, L. S. Mason, H. L. Tuller and D. R. Uhlmann: Solid State Ionics 9/10 (1983) 585.
[5] K. Funke: Sol. State Ionics 94 (1997) 27.
[6] P. Znášik and M. Jamnický: Solid St. Ionics 95 (1997) 207.
[7] M. Cutroni, A. Mandanici: Solid State Ionics 105 (1998) 149.
[8] D. P. Almond, A. R. West: Solid State Ionics 26 (1988) 265.
[9] G. Carini, M. Cutroni, M. Federico, G. Galli and G. Ttipodo: Physical Review B 30 (1984) 7219.
[10] L.Börjesson: Physical Review B 36 (1987) 4600.
[11] B. Roling and M. D. Ingram: Physical Review B 57 (1998) 14192.
[12] P. Bury, P. Hockicko, M. Jamnický and I. Jamnický: Advances in Electrical and Electronic Engineering, Vol. 2/2003, No. 3-4, 16.
[13] P. Bury, P. Hockicko, M. Jamnický and I. Jamnický: Proc. of the 18th International Congress on Acoustics, Kyoto 2004, (will be published).