Harmonický oscilátor
Následující tvrzení jsou pro harmonický oscilátor charakteristická, každé
z nich lze chápat jako definici harmonického oscilátoru. Tvrzení jsou navzájem
ekvivalentní.
|
| Wp
= 1/2 k y 2 |
Systém má parabolickou závislost potenciální energie. Má-li
průběh potenciální energie minimum, bude systém vždy vykonávat kmity. Potenciální
energii s minimem lze pro malé výchylky nahradit parabolou a libovolný
systém s minimem potenciální energie tak aproximovat harmonickým oscilátorem
(prohlédněte si příklad "Morseův potenciál"
nebo "Oběh Země kolem Slunce"). Význam k:
k = Wp" v minimu, konstanta udává strmost paraboly
či tuhost oscilátoru. |
| F = - ky |
Síla je úměrná výchylce z rovnovážné polohy a má opačný směr.
Tento vztah plyne z předchozího okamžitě (F = - dWp/dy). |
| d2y/dt2
+ w02 y = 0 |
Systém se řídí diferenciální rovnicí pro kmity: Tento vztah
odvodíme z předcházejícího z pohybové rovnice (m d2y/dt2
= F) . Mezi frekvencí a tuhostí platí vztah w02
= k/m. |
y(t) = c1
eiw
t + c2 e-iw
t
y(t) = a cos (wt) + b sin (wt)
y(t) = A cos (wt
+ j) . |
Systém kmitá periodicky podle některé z těchto závislostí. Všechna
vyjádření jsou řešením diferenciální rovnice harmonických oscilací a jsou
vzájemně ekvivalentní. Mezi dvojicemi integračních konstant (c1, c2), (a, b), (A, j)
existují jednoduché převody. |
Tlumené kmity
|
d2y/dt2 + 2d
dy/dt + w02 y = 0 |
Tlumený oscilátor splňuje diferenciální rovnici kmitů doplněnou o člen
s útlumem. |
| y(t) = A0
e-d t cos (wt
+ j) |
Řešení rovnice tlumených kmitů. |
| w2
= w02 - d2 |
Kvadrát frekvence tlumených kmitů. |
| A(t) = A0
e-d t |
Exponenciální pokles amplitudy A(t) u tlumeného kmitu. |
| E(t) = E0
e-2d t |
Celková energie je úměrná kvadrátu amplitudy a proto klesá podle tohoto
vztahu. |
| d |
Koeficient útlumu. |
| L = dT |
Logaritmický dekrement útlumu. |
Vynucené kmity
|
d2y/dt2 + 2d
dy/dt + w02 y =
= F0/m exp(i
Wt) |
Vynucený oscilátor splňuje rovnici tlumených oscilací doplněnou o vnější
periodickou sílu o frekvenci W. V principu může
být vnější síla jakákoli. Vzhledem k tomu, že problém je lineární, můžeme
libovolnou sílu složit z harmonických sil typu exp(iWt). |
| y(t) = A0
e-d t cos (wt+j) + A exp(iWt) |
Řešení rovnice vynucených kmitů. První člen je řešení homogenní rovnice,
představuje tlumený kmit, který postupně ustane. Jde tedy jen o přechodový
jev. Druhý člen je partikulární řešení, které bude jediným nenulovým
řešením po dosti dlouhé době. Jde o vynucený kmit s frekvencí vnější síly.
Amplituda je obecně komplexní číslo, které způsobuje fázový posun vynuceného
kmitu oproti vnější síle. |
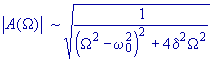 |
Velikost amplitudy vynucených oscilací. |
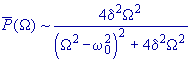 |
Velikost střední hodnoty přeneseného výkonu. |
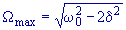 |
Amplitudová rezonance. Podmínka maximální amplitudy vynucených
kmitů. |
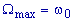 |
Výkonová rezonance. Podmínka pro maximální přenesený výkon.
Maximální amplituda vynucených kmitů (amplitudová rezonance) tedy nastává
při jiné frekvenci vnější síly než maximum přeneseného výkonu (výkonová
rezonance) Prohlédněte si příklad "Amplitudová
a výkonová rezonance". |
Skládání kmitů
Je-li systém lineární, platí princip superpozice a kmity lze
skládat. Obecné kmity můžeme psát jako superpozici několika základních
modů. Kmitá-li celý komplikovaný systém na jedné jediné frekvenci, hovoříme
o tzv. vlastní frekvenci. Systémy zpravidla mají několik různých
vlastních frekvencí. Při skládání kmitů ve stejném směru vznikají pro dvě
blízké frekvence rázy (prohlédněte si příklad "Skládání
kmitů, vlastní frekvence", prohlédněte si aplet "Rázy"). Při skládání kmitů ve dvou navzájem kolmých
směrech vznikají pro frekvence v poměru malých celých čísel tzv. Lissajousseovy
obrazce.
|







